44. Преобразование декартовых прямоугольных координат на плоскости и в пространстве
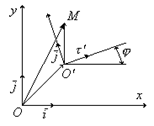 Пусть на плоскости заданы две произвольные декартовы прямоугольные системы координат. Первая определяется началом О и базисными векторами I J , вторая – центром О’ и базисными векторами I’ J’.
Пусть на плоскости заданы две произвольные декартовы прямоугольные системы координат. Первая определяется началом О и базисными векторами I J , вторая – центром О’ и базисными векторами I’ J’.
Поставим цель выразить координаты x y некоторой точки М относительно первой системы координат через X’ и Y’ – координаты той же точки относительно второй системы.
Заметим, что 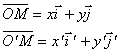
Обозначим координаты точки О’ относительно первой системы через a и b:
![]()
Разложим векторы I’ и J’ по базису I J:
![]() (*)
(*)
Кроме того, имеем: ![]() . Введем сюда разложения векторов по базису I’ J’:
. Введем сюда разложения векторов по базису I’ J’:
![]()
Отсюда ![]()
Можно сделать вывод: каковы бы ни были две произвольных декартовы системы на плоскости, координаты любой точки плоскости относительно первой системы являются линейными функциями координат той же точки относительно второй системы.
Умножим скалярно уравнения (*) сначала на I, затем на J:
![]() (**)
(**)
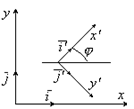 Обозначим через j угол между векторами I и I’. Система координат I J может быть совмещена с системой I’J’ путем параллельного переноса и последующего поворота на угол j. Но здесь возможен и дугой вариант: угол между базисными векторами I I’ также j, а угол между базисными векторами J’J’ равен p - j. Эти системы нельзя совместить параллельным переносом и поворотом. Необходимо еще и изменить направление оси у На противоположное.
Обозначим через j угол между векторами I и I’. Система координат I J может быть совмещена с системой I’J’ путем параллельного переноса и последующего поворота на угол j. Но здесь возможен и дугой вариант: угол между базисными векторами I I’ также j, а угол между базисными векторами J’J’ равен p - j. Эти системы нельзя совместить параллельным переносом и поворотом. Необходимо еще и изменить направление оси у На противоположное.
Из формулы (**) получаем в первом случае:

Во втором случае

Формулы преобразования имеют вид:
I. ![]()
II. ![]()
Второй случай мы рассматривать не будем. Условимся считать обе системы правыми.
Т. е. вывод: каковы бы ни были две правые системы координат, первая из них может быть совмещена со второй путем параллельного переноса и последующего поворота вокруг начала на некоторый угол j.
Формулы параллельного переноса: ![]()
Формулы поворота осей: ![]()
Обратные преобразования:
![]()
| < Предыдущая | Следующая > |
|---|