43. Рассмотрим некоторые примеры задач на прямую и плоскость в пространстве

1). Условия пересечения трех плоскостей в одной точке:

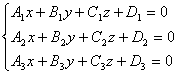
Очевидно, для единственности решения необходимо и достаточно, чтобы определитель .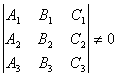

2). Уравнение прямой, проходящей через данную точку M1(X1 Y1 Z1) и перпендикулярную данной плоскости A X + B Y + C Z + D = 0.

Т. к. направляющим вектором некоторой прямой является вектор . Тогда каноническое уравнение искомой прямой есть.

3). Уравнение плоскости, проходящей через заданную точку M0(X0 Y0 Z0) и перпендикулярной заданной прямой :

Вспомним уравнение связки плоскостей, т. е. уравнение всех плоскостей, проходящих через точку X0 Y0 Z0:

A (X – X0) + B (Y – X0) + C (Z– X0) = 0.

Искомая плоскость в качестве нормали имеет направляющий вектор заданной прямой . В итоге получаем уравнение: L (X – X0) + M (Y – X0) + N (Z– X0)=0.

4). Уравнение плоскости, проходящей через данную прямую и через точку, не лежащую на этой прямой M0(X0 Y0 Z0).

Искомая плоскость принадлежит связке: A (X – X0) + B (Y – X0) + C (Z– X0) = 0.

С другой стороны, этому уравнению должны удовлетворять координаты точки x1, y1, z1:

Вспомним условие принадлежности прямой к плоскости:

И получим в итоге:

Отсюда, выразив два коэффициента из А В С через третий, можно найти уравнение плоскости.

Другой способ: найти векторное произведение направляющего вектора и вектора Координаты этого вектора будут, очевидно, координатами нормального вектора к искомой плоскости. Для окончательного написания уравнения плоскости необходимо использовать уравнение связки плоскостей - плоскостей, проходящих через точку М0.

5). Уравнение перпендикуляра, опущенного из заданной точки M0 на данную прямую L1.

Искомый перпендикуляр – это линия пересечения двух плоскостей: 1) плоскость, проходящая через точку M0 и прямую L1 – предыдущий пример и 2) плоскость, проходящая через M0 и перпендикулярную L1 – это задача № 3. Решая совместно эти два условия, найдем искомое уравнение прямой.

Другой способ: построить плоскость p, проходящую через точку М0 и перпендикулярную прямой L1. Далее найти точку пересечения плоскости p и прямой L1. Предположим, это будет некоторая точка С. Искомым расстоянием будет длина вектора .

6). Нахождение расстояния от данной точки M0 до данной прямой L1.

Надо совместно решить уравнения прямых L1 и L2 – это уравнение перпендикуляра из предыдущей задачи № 5, таким образом найдем координаты точки пересечения прямых L1 и L2 - основания перпендикуляра M2. Расстояние – это модуль вектора .

Другой путь решения задачи:

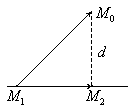L1: q={l, m,n}

Расстояние от точки М0 до прямой L1 есть площадь параллелограмма деленная на основание Q:

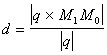
7) Найти расстояние между двумя скрещивающимися прямыми:

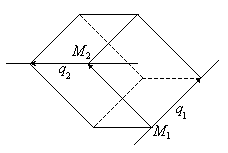L1: L2:

Расстояние равно объему параллелепипеда, построенного на сторонах Q1, Q2, M1M2, деленному на площадь основания

< Предыдущая		Следующая >