46. Поверхности второго порядка
Поверхностью второго порядка будем называть геометрическое место точек в пространстве, удовлетворяющих уравнению:
![]()
Где по крайней мере один из A11 A22 A33 ¹ 0. Это уравнение называется общим уравнением поверхности второго порядка.
Назовем группу слагаемых ![]() группой старших членов, а
группой старших членов, а ![]() - линейной частью. A44 – свободный член.
- линейной частью. A44 – свободный член.
Перейдем к новой системе координат с целью упростить общее уравнение.
Сначала осуществим параллельный перенос:

Подставив в общее уравнение, получим:
![]() Где
Где  (*)
(*)
Важный вывод: при параллельном переносе системы координат коэффициенты при старших членах не изменяются! Преобразуются коэффициенты группы линейных членов по некоторым формулам.
Рассмотрим поворот осей:
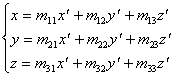
Если введем эти координаты в общее уравнение поверхности, сгруппируем члены при различных степенях x’ y’ z’ и получим:
![]()
Легко убедиться, если расписать коэффициенты ![]() и т. д., что: при повороте сисемы координат коэффициенты старших членов зависят лишь от Mij и старых коэффициентов старших членов, а коэффициенты
и т. д., что: при повороте сисемы координат коэффициенты старших членов зависят лишь от Mij и старых коэффициентов старших членов, а коэффициенты ![]() - зависят только от Mij И
- зависят только от Mij И ![]() , а
, а ![]() не изменяется! При этом, если в исходном уравнении коэффициенты
не изменяется! При этом, если в исходном уравнении коэффициенты ![]() были равны нулю, то и
были равны нулю, то и ![]() будут равны нулю! Другими словами, при параллельном переносе можно упрощать группу линейных членов, а при повороте – упрощать группу старших членов уравнения.
будут равны нулю! Другими словами, при параллельном переносе можно упрощать группу линейных членов, а при повороте – упрощать группу старших членов уравнения.
Оказывается, существуют инварианты относительно любого преобразования системы. Это величины:
![]()

| < Предыдущая | Следующая > |
|---|