21. Выражение векторного произведения в декартовых координатах

Если два вектора имеют координаты , то их векторное произведение можно найти, опираясь на свойства векторного произведения:

В итоге (*)

Или 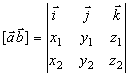- разложение определителя по первой строке.

Следствие. Если два вектора Коллинеарны, то координаты их пропорциональны. Действительно, векторное произведение коллинеарных векторов равно нулю. Но из равенства (*) следует (поскольку ): .

< Предыдущая		Следующая >