19. Смешанное произведение трёх векторов

Если вектор векторно умножается на вектор , затем получившийся вектор скалярно умножается на вектор , то в результате получается число , называемое смешанным произведением векторов .

Теорема. Смешанное произведение равно объёму параллелепипеда, построенного на векторах И взятому со знаком плюс, если тройка - правая, и минус если тройка левая. Докажем для правой тройки:

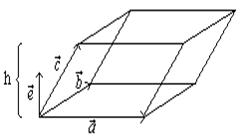
Следствие 1: Справедливо равенство: . Доказанное равенство позволяет записывать смешанное произведение, не указывая при этом, какое произведение векторное, какое скалярное. Обозначается смешанное произведение .

Следствие 2: Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.

Следствие 3: Смешанное произведение трёх векторов, два из которых совпадают, равно нулю. В самом деле, такие векторы колмпланарны заведомо.

< Предыдущая		Следующая >