18. Векторное и смешанное произведения векторов

Прежде всего назовём три вектора упорядоченной тройкой, если указано, какой вектор называется первый, второй и третий. Так, запись Означает, что

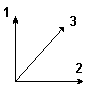- правая тройка

Определим правую систему координат по правилу правой руки или по правилу буравчика.

Определение: аффинная система координат называется правой, если три базисных вектора образуют правую систему координат.

Определение векторного произведения: векторным произведением вектора На вектор Называется вектор , обозначаемый И удовлетворяющий требованиям:

1) длина вектора Равна: ;

2) вектор Ортогонален каждому из И ;

3) Направлен так, что -правая тройка.

Понятие векторного произведения родилось тоже в механике.

-момент М силы Относительно точки О.

Теорема. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

Необходимость вытекает из самого определения векторного произведения.

Достаточность. Пусть . Тогда и , и остаётся , т. е. коллинеарность

Теорема. Модуль векторного произведения равен площади параллелограмма, построенного на приведённых к общему началу векторах . Эта теорема непосредственно вытекает из формулы .

< Предыдущая		Следующая >