17. Алгебраические свойства скалярного произведения

1). переместительное свойство.

2). сочетательное относительно числового множителя.

3). распределительное относительно суммы векторов.

4). Если и , если .

Докажем, допустим, свойство 2: .

Эти четыре свойства позволяют при скалярном перемножении векторных многочленов выполнить действия почленно, не заботясь о порядке и сочетая числовые множители. Используем эти свойства практически. Найдём выражение скалярного произведения в декартовых координатах.

Если два вектора , то их скалярное произведение есть

.

Для доказательства составим скалярные произведения:

И запишем: .

Следствие 1. Необходимое и достаточное условие ортогональности двух векторов является равенство .

Следствие 2. Угол между двумя векторами есть:

.

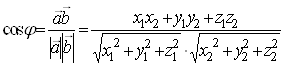< Предыдущая		Следующая >