15. Понятие базиса

Говорят, что три линейно независимых вектора И Образуют в пространстве базис, если любой вектор Может быть представлен в виде линейной комбинации векторов

(**)

Принято называть (**) разложением вектора d по базису , а числа -координатами вектора Относительно базиса . Причём можно доказать, что разложение По базису может быть единственным образом осуществлено.

Определим так называемые Афинные координаты. Афинные координаты в пространстве определяются заданием базиса и некоторой точки О, называемой началом координат.

Частным случаем афинных координат являются, очевидно, прямоугольные декартовы координаты, Здесь введём три взаимно перпендикулярных (ортогональных) единичных векторов . Для каждого вектора Найдётся и при том единственная тройка чисел , такая, что

Числа X, Y,Z называют декартовы прямоугольные координаты.

Введём определение проекции вектора на ось V. Дан вектор . Опустим перпендикуляры из точек А и В на ось V. Основания перпендикуляров обозначим И .

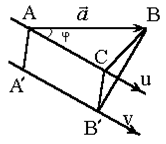
Проекцией вектора На ось V назовём величину направленного отрезка оси V.

Углом наклона вектора к оси V назовём угол между направлением вектора и направлением оси V. Из рассмотрения треугольника АВС следует, что .

Можно доказать, что декартовы координаты X, Y,Z вектора Являются проекции вектора На оси соответственно ортам:

-ось Ох, -ось Oy, - ось Oz.

Или можно записать:

(***)

Три числа называются направляющими косинусами вектора .

Длина диагонали параллелепипеда равна

Тогда можно записать:

Возведём в квадрат и складывая, получим равенство:

.

< Предыдущая		Следующая >