14. Линейные комбинации трёх векторов

Определение: векторы называются компланарными, если они лежат в одной плоскости, либо в параллельных плоскостях.

Теорема 5. Необходимым и достаточным условием линейной зависимости трёх векторов является их компланарность.

Необходимость: пусть три вектора линейно зависимы:

.

Тогда , или

Это равенство означает сложение двух векторов, т. е. все три вектора лежат в одной плоскости.

Достаточность: пусть компланарны. Исключим случай, когда пара векторов коллинеарна и когда какой-либо вектор равен 0. Эти случаи тривиальны. Рассмотрим случай, когда все неколлинеарны.

Перенесём все векторы в одну плоскость. Поскольку они неколлинеарны, то существует их общая точка пересечения:

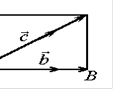
В силу теоремы 1, найдутся такие И , что

Или . Теорема доказана.

Следствие: Если векторыИНеколлинеарны, то для любого , лежащего в одной плоскости с векторами И Найдутся такие И, что выполнится равенство:

Наконец, Линейная зависимость трёх векторов.

Теорема 6. Любые четыре вектора линейно зависимы.

Доказательство. Исключим тривиальные случаи, когда один из векторов ноль или когда какие-либо три компланарны. По предыдущим теоремам будут линейно зависимы все четыре вектора. Т. е. все векторы некомпланарны. Сведём их в одну точку и построим параллелепипед:

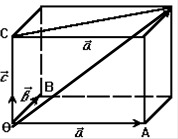
По теореме 1 найдутся такие числа, что:

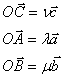
Но вектор Равен или или .

Теорема доказана.

Попутно мы доказали, что если , какие-либо некомпланарные, т. е. линейно независимые векторы, то для любого вектора можно найти такие числа , что

.

< Предыдущая		Следующая >