12. Понятие вектора

Существуют величины, которые характеризуются помимо своей величины ещё и направленностью. Это скорость, ускорение, сила, смещение материальной точки и т. п. Можно абстрагироваться от конкретной физической величины и считать, что вектор - это направленный отрезок. Определение: вектор - это направленный отрезок.

Будем обозначать вектор AB. А - начало вектора, В - конец вектора.

- означает длина вектора (символ модуля).

Вектор называется нулевым, если его начало и конец совпадают.

Важное свойство векторов - коллинеарность. Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Теперь сформулируем понятие равенства двух векторов: два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление. Два нулевых вектора считаются равными.

равные неравные

Из определения равенства векторов следует, что мы не различаем двух равных векторов, имеющих разные точки приложения. Иными словами, точка приложения вектора может быть произвольной. В соответствии с этим векторы в геометрии называются свободными.

Определим линейные операции над векторами.

Сложение. Суммой двух векторов Называется вектор, идущий из начала вектора в конец вектора при условии, что начало приложено к концу вектора .

Геометрически это можно изобразить правилом треугольника:

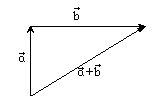
Правило сложения векторов обладает теми же четырьмя свойствами, что и правило сложения вещественных чисел:

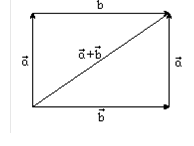
1. (переместительное свойство).

2. (сочетательное свойство).

3. Существует нулевой вектор, такой, что .

4. Для каждого существует такой что .

Эти свойства доказываются геометрическими построениями. К примеру свойство 1:

Эти свойства позволяют оперировать с векторами так же как и с вещественными числами.

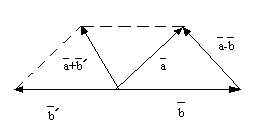Определим разность векторов

как сумму

где

- противоположный вектор вектору

Определим, наконец, операцию умножения вектора на вещественное число.

Произведением называется вектор, коллинеарный , имеющий длину и имеющий направление, совпадающее с если И противоположное, если .

Геометрический смысл умножения - вектор растягивается в раз.

Операция умножения обладает тремя свойствами:

5. (распределительное свойство относительно суммы векторов).

6. (распределительное свойство относительно суммы чисел).

7. (сочетательное свойство).

Доказываются эти свойства тоже графически.

Рассмотрим Теорему 1. Если вектор Коллинеарен вектору , то существует такое вещественное число , что .

Совместим И . В силу коллинеарности они окажутся на одной прямой. Т. е.

(*)

Докажем, что . Т. е. что длины их равны, направления совпадают, коллинеарны.

Коллинеарность вытекает из определения произведения И коллинеарности И , равенство длин непосредственно из определения произведения и (*). Наконец, опять из определения произведения следует, что если , направления совпадают, и если , то И - противоположно направлены.

Определение 1. Линейной комбинацией n векторов мы называем сумму вида

Где - вещественные числа.

Определение 2. Векторы называются линейно зависимыми, если существуют такие , хотя бы одно из которых отлично от нуля, что имеет место равенство:

Если все , то такие векторы называются линейно независимыми.

Докажем Теорему 2. Если среди N Векторов хотя бы один нулевой, то эти векторы являются линейно зависимы. Доказательство: пусть для определённости . Тогда выполняется равенство:

Где .

И по определению линейной зависимости эти векторы линейно зависимы.

Теорема номер три: если среди П Векторов Какие либо (П-1) линейно зависимы, то и все П являются линейно зависимы.

Действительно: линейная зависимость (П-1) векторов означает:

Добавим сюда равное 0 слагаемое и получим ,

Где не все равны нулю, т. е. теорема доказана.

< Предыдущая		Следующая >