11. Однородная система линейных алгебраических уравнений
Матричная запись АХ=0
Расширенная матрица отличается от матрицы самой системы наличием нулевого столбца, т. е. ранг матрицы А rang A равен рангу расширенной матрицы rang B.
ra=rb
Значит, по теореме Кронеккера-Капелли, система однородных линейных уравнений всегда совместна. Одно решение очевидно: xi=0 (i=1,...,n). Это решение называется тривиальным. Следуя далее теореме Кронеккера-Капелли, придём к выводу, что если rA=n, то решение единственное - тривиальное. Если rA<n, то решений бесконечное множество. Рассуждая таким образом, мы доказали следующую теорему:
Для того, чтобы система однородных уравнений имела решения, отличные от нулевого, необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных. Другими словами, если число уравнений равно числу неизвестных, то система имеет ненулевое решение тогда и только тогда, когда detA=0.
Очевидны следующие свойства ненулевого решения:
1). Если ![]() - решение, то
- решение, то ![]() - тоже решение.
- тоже решение.
2). Если ![]() - решения, то и
- решения, то и ![]() - тоже решения.
- тоже решения.
В действительности этих свойств можно убедиться непосредственной подстановкой.
Обозначим главные неизвестные через х1 ,...,х2. Тогда, аналогично (****):
 В матричной форме:
В матричной форме: 
Можно записать так:
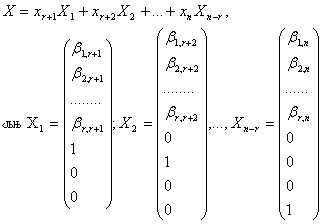
Решения X1,X2,…,Xn-r называются фундаментальной системой решений однородной системы. Общее решение системы X является линейной комбинацией фундаментальной системой решений
X=c1X1+c2X2+...+cn-rXn-r.
Пример:
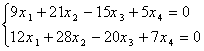
![]()
![]()
![]()
![]()
![]()
![]()
![]()
За главные неизвестные необходимо выбирать такие, при которых матрица коэффициентов не вырождена, т. е. ее определитель не равен нулю.
Возьмём за главные неизвестные х1 и х4, поскольку х1 и х2 ![]()
Тогда ![]()
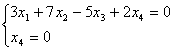
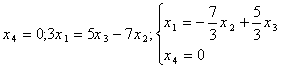
Фундаментальная система решений:
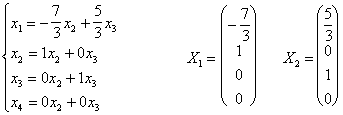
Общее решение:
X=с1X1+с2X2
| < Предыдущая | Следующая > |
|---|