10. Системы линейных уравнений
Рассмотрим в общем случае решение систем линейных уравнений. Дадим несколько определений.
1). Системой m уравнений с n неизвестными называется система вида:
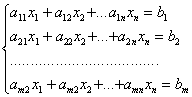 (**)
(**)
2). Если в системе (**) все bк (k=1,...m) равны нулю, то такая система называется однородной.
3). Если хотя бы один из них bк![]() 0, то система называется неоднородной.
0, то система называется неоднородной.
4). Система (**) называется совместной, если она имеет хотя бы одно решение, в противном случае она называется несовместной.
5). Совместная система линейных уравнений называется определённой, если она имеет единственное решение и неопределённой - если решений множество.
Итак, начнём с помощью элементарных преобразований сводить расширенную матрицу системы уравнений (**) к треугольному виду. Прежде всего, здесь количество уравнений не равно количеству неизвестных. Значит матрица прямоугольная и вообще говоря, к треугольной не сводится. Второй момент: Вспомним о ранге матрицы. Ранг матрицы равен количеству ненулевых строк в ступенчатой матрице, которая получится из исходной элементарными преобразованиями. Т. е. некоторые строки преобразованной матрицы могут остаться нулевыми. В итоге, после учёта этих моментов, можно записать самый общий вид преобразованной матрицы, который только может встретиться:
 (***)
(***)
Или, условно нарисуем:
Обратим внимание на коэффициент ![]() . Может случиться, что это будет 0. А может и нет. Тогда
. Может случиться, что это будет 0. А может и нет. Тогда ![]() , что невозможно. Значит решений нет, т. е. система несовместна. Поэтому на практике, сразу же после появления соотношения вида
, что невозможно. Значит решений нет, т. е. система несовместна. Поэтому на практике, сразу же после появления соотношения вида ![]() можно говорить, что система не имеет решения.
можно говорить, что система не имеет решения.
Если ![]() , то, покажем, что система имеет решение. Поскольку
, то, покажем, что система имеет решение. Поскольку ![]() , то из последнего уравнения можно найти
, то из последнего уравнения можно найти
![]() или
или ![]() [
[![]() ] Из предыдущего уравнения можно найти
] Из предыдущего уравнения можно найти
![]() [
[![]() ]
]
И т. д. В итоге:
 (****)
(****)
Из этих соотношений следует, что xr+1,...,xn могут принимать произвольные значения. Эти неизвестные называются свободными, а x1,...xr - называются основными или главными. Любая совокупность свободных неизвестных и соответствующих им основных будет решением системы. Таким образом, мы доказали теорему:
Теорема Кронекера-Капелли: для того, чтобы система уравнений (**) была совместной, необходимо и достаточно, чтобы ранг матрицы этой системы и ранг расширенной матрицы были равны. Далее, предположим мы выяснили, что система уравнений совместна. Тогда возможны два случая:
1) ранг матрицы равен количеству неизвестных R=N. Это возможно, кстати, при m![]() N. В этом случае все неизвестные главные и они равны из (****):
N. В этом случае все неизвестные главные и они равны из (****):
![]()
Это означает, что система имеет единственное решение. Система определённая.
2) r<n. В этом случае имеются свободные неизвестные, которые можно задавать произвольно. Значит система имеет бесконечное множество решений, т. е. система неопределённая!
Пример:
![]()
![]()
![]()
![]() 1)
1) 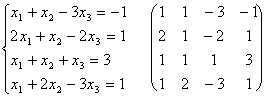
![]()
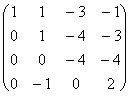
![]()

![]()
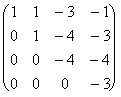 0 = -3 !!!
0 = -3 !!!
Система несовместна, решений нет!
2)
![]()
![]()

![]()

![]()
![]()
![]()

![]()
Система совместна. Положим x3=c1, x4=c2 , тогда:

Бесконечное множество решений.
| < Предыдущая | Следующая > |
|---|