05. Свойства определителей

1. Величина определителя не изменится, если строки и столбцы поменять местами, т. е. транспонировать матрицу. Доказать можно, расписав определители:

2. Перестановка двух строк или двух столбцов определителя равносильна его умножению на (-1). Для доказательства достаточно расписать определитель:

.

3. Если определитель имеет две равные строки или два равных столбца, то он равен 0. Это очень важное свойство. В самом деле, перестановка строк даёт: .

4. Умножение всех элементов некоторой строки на число равносильно умножению определителя на это число . Иными словами, общий множитель из некоторой строки можно выносить за знак определителя:

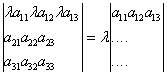
5. Отсюда вытекает, что если все элементы некоторой строки =0, то и сам определитель равен 0.

6. Если элементы двух строк пропорциональны, то определитель равен 0.

7. Проще написать на доске:

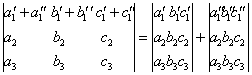
8. Если к элементам одной строки прибавить элементы другой строки, умноженной на некоторый коэффициент , то величина не изменится!

9. Непосредственно из выражения определителя следует, что величина определителя равна сумме произведений элемента на алгебраическое дополнение этого элемента.

Обратным образом: сумма произведений элементов какого-либо столбца на алгебраические дополнения другого столбца равна нулю.

Если ввести обозначение и назвать АIj алгебраическим дополнением элемента АIj , то последнее свойство (9) можно записать

,

Где - символ Кронекера:

< Предыдущая		Следующая >