04. Определители
Мы уже ввели понятие определителя для матрицы 3-го порядка. Перейдём теперь к понятию определителя порядка n, где ![]() .
.
Введём понятие минора. Минором любого элемента ![]() матрицы n-ого порядка называется определитель порядка n-1, соответствующий матрице, полученной из родительской матрицы вычёркиванием i-той строки и j-того столбца. Обозначим минор символом
матрицы n-ого порядка называется определитель порядка n-1, соответствующий матрице, полученной из родительской матрицы вычёркиванием i-той строки и j-того столбца. Обозначим минор символом ![]() (Лучше обозначить просто Мij)
(Лучше обозначить просто Мij)
![]()
![]()

К примеру у матрицы четвёртого порядка можно выделить 16 миноров:

Запишем теорему без доказательства:
Теорема 1. Каков бы ни был номер строки i (i=1,...n); для определителя n-ого порядка справедлива формула:
![]()
Эта формула называется разложением определителя по i-той строке.
Подчеркнём, что в этой формуле показатель степени, в которую возводится (-1) равен сумме номеров строки i и столбца j, т. е. сумма может быть чётной и нечётной. Соответственно слагаемые в этой сумме могут входить в неё как со знаком (+) так и со знаком (-). Пример : (разложим по 2-й строке)
 Кстати, проще разложить по третьей строке:
Кстати, проще разложить по третьей строке:
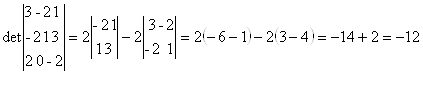
К этому же результату можно прийти, воспользовавшись формулой ****) - знаменатель при вычислении х3, иначе называемой формулой “треугольника”:
![]()
| < Предыдущая | Следующая > |
|---|