03. Операции над матрицами

Матрицы считаются равными, если они имеют одинаковые порядки и их соответствующие элементы совпадают.

А). Сложение матриц. Суммой двух матриц И одних и тех же порядков называют матрицу , элементы которой есть

Будем писать: С=А+В

Непосредственно из определения вытекает :

Переместительное свойство А+В=В+А

И сочетательное свойство (А+В)+С=А+(В+С)

Б). Умножение матрицы на число : матрица умножается на число , получается матрица - (каждый член умножается на). Отсюда непосредственно следует:

сочетательный закон:

Распределительный закон относительно суммы чисел:

В). Перемножение матриц: произведением двух матриц и называют матрицу , где определяется из формулы:

Т. е. не всякие матрицы можно перемножить а только те, где число столбцов матрицы А равно числу строк матрицы В.

Частный случай - умножение матрицы-строки на матрицу-столбец определено, если количество членов в строке (n) равно количеству членов в столбце (n). Результатом такого умножения является число

n

x В n = С11

А

Определено всегда умножение столбца на строку:

n

M x = m

n

Произведение двух матриц не обладает перестановочным свойством, т. е. . К примеру:

Введём важное понятие диагональной матрицы

И её частный случай - единичную матрицу:

Легко увидеть, что для любой квадратной матрицы А справедливо :

Познакомившись с умножением матриц, можно нашу систему уравнений ***) записать компактно в матричном виде. Введём обозначения. Матрицу системы уравнений, представляющую таблицу из коэффициентов при неизвестных, обозначим А:

.

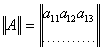Для неизвестных введём обозначения матрицы-столбца Х

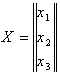
И для правых частей - .

Тогда можно записать:

Или

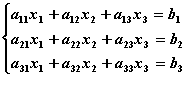
< Предыдущая		Следующая >