02. Матрицы. Линейные операции над ними. Умножение матриц

Прежде чем начать изучение матриц, вспомним, что такое определитель. Рассмотрим простую задачу:

Решить систему двух уравнений с двумя неизвестными:

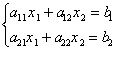
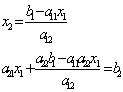выразим неизвестную x2 из первого у-я (*)

Её решение, как известно, выглядит:

(**)

Запишем систему трёх уравнений:

***)

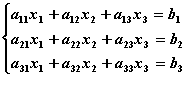Запишем первые два уравнения так:

И решим по формулам (**):

Подставим в третье уравнение и решим его:

Аналогично можно записать решение для х1 и х2, которые мы здесь опустим.

Числитель можно получить из знаменателя простой заменой членов На ! Т. е. при решении системы трёх уравнений всё определяется знаменателем. Запишем алгебраические члены, входящие в выражение в знаменателе как таблицу

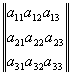
Эту таблицу назовём матрицей системы уравнений (***), а выражение в знаменателе - определителем этой матрицы. Для числителя аналогичная таблица чисел выглядит

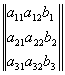
Обозначив определитель матрицы системы уравнений через D, а числитель через Di, получим для разыскиваемых хi простую формулу, называемую правилом Крамера

Xi = Di / D

Оказывается, эта формула верна для системы уравнений любого порядка.

Таким образом, для решения системы уравнений достаточно найти определитель матрицы этой системы и сделать некоторые преобразования с определителем.

Абстрагируемся от систем уравнений и назовём матрицей вообще некоторую прямоугольную таблицу чисел. Причём число строк и столбцов может быть и неодинаковым! Запишем в общем виде:

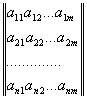
Употребляют и сокращённую запись:

где i=1,... n; j,... m

Или вообще просто: A (будем употреблять мы).

Числа n и m назовем порядками матрицы n ´ m (n строк на m столбцов). Например матрица 2 ´ 2; 2 ´ 3 и т. п.

В случае квадратной матрицы вводится понятие главной диагонали. Это элементы аii

Частные случаи: Матрица - столбец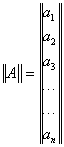

Матрица - строка

Транспонирование матрицы - это операция перестановки строк и столбцов. Обозначается операция : Т

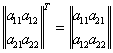
Очевидно, что транспонированная матрица-строка - это матрица-столбец и наоборот. Особую роль играют матрицы, которые при транспонировании не изменяются. Такие матрицы называются симметрическими. Бывают ленточные матрицы с шириной диагонали - k членов. Для симметрических матриц можно говорить о полуширине диагонали.

< Предыдущая		Следующая >