01. Что такое алгебра?

Что такое алгебра? Исторически алгебра сложилась как наука о решении уравнений. Ещё в древнем Вавилоне 4000 лет назад люди уже умели решать квадратные уравнения. Это умение возникло из практической необходимости решать задачи земледелия, строительства, военного искусства. К примеру, на одной из глиняных табличек, относящихся к тому времени учёные историки расшифровали задачу:

Площадь двух квадратов равна 1000. Сторона одного квадрата составляет две трети стороны другого, уменьшенные на 10. Каковы стороны квадратов?

Эта задача приводит к системе уравнений:

Которая сводится к квадратному уравнению:

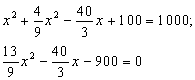
Отсюда x=30, а y=10.

Разумеется, система записи математических соотношений была иной.

Само название “алгебра” восходит к арабским учёным. В 825 году был написан учебник “Краткая книга об исчислении ал-Джабра”. “Ал-Джабра” в переводе означает перенос или восполнение. Автор учебника – выдающийся ученый Мухаммед бен Муса аль-Хорезми. (Кстати, слово «алгоритм» произошло от латинской формы имени аль-Хорезми). Этот термин и стал названием науки. По этой книге долгое время обучалась вся Европа. Прошли столетия и в настоящее время алгебра оформилась как наука, предметом которой являются операции, записанные в символической форме. Над чем осуществлялись операции? Над математическими моделями. Такими моделями в современной алгебре являются группы, кольца, поля, векторные пространства и т. д.

Предметом нашего изучения в курсе “линейной алгебры” являются матрицы, линейные пространства, системы линейных уравнений и др. Кроме того, мы в рамках “линейной алгебры” будем изучать геометрические объекты: вектора, уравнения линий и кривых на плоскости и в пространстве, поверхности 2-го порядка. Сам термин “линейная” означает, что над объектами изучения вводятся, т. е. определены три операции: сложение и умножение в пространстве объектов и умножение объектов на скаляр. Для определения линии в пространстве достаточно этих операций. От линии и происходит термин “линейная”.

Для чего нужен этот курс математики? Применительно к будущей специальности инженер-механик мы приведём только один пример. При создании современных машин, приборов и т. п. приходится проводить расчёты на прочность конструкций. Существует мощный современный метод - метод конечных элементов - позволяющий решать задачу расчёта на прочность сложных конструкций.

Математически этот метод сводится к решению большой системы уравнений с большим числом неизвестных. При составлении и решении этих систем уравнений интенсивно используется аппарат линейной алгебры как фундамент или основа для более сложных математических преобразований.

Одним из объектов, изучаемых в курсе линейной алгебры являются матрицы. Тема первой лекции так и называется:

Следующая >