06. Обратная матрица

Пусть А - квадратная матрица. Определение: Матрица В называется обратной левой матрицей по отношению к матрице А, если

Матрица С называется обратной правой по отношению к А, если

.

Убедимся, что если матрицы В и Е существуют, то они совпадают между собой. Действительно:

Таким образом правые и левые матрицы совпадают и они называются просто обратная матрица и обозначаются А-1. Вспомним оговорку “... если существует обратная матрица”. Какие условия следует наложить на матрицу А, чтобы существовала у неё обратная матрица?

Теорема. Для того, чтобы для матрицы А существовали левая и правая обратные матрицы, необходимо и достаточно, чтобы определитель det А матрицы А был отличен от нуля.

Необходимость: допустим матрица В существует. Тогда из соотношения АВ=Е следует: . Значит .

Здесь мы использовали свойство определителей: определитель произведения матриц равен произведению определителей этих матриц. Примем это без доказательства.

Достаточность. Пусть определитель detA=. Составим следующую матрицу В:

Здесь через обозначены алгебраические дополнения соответствующих элементов .Убедимся, что она обратная. Умножим:

Эта сумма есть не что иное, как разложение определителя матрицы по первой строке, и значит, эта сумма =.

Эта сумма является суммой произведений элементов второй строки матрицы А на алгебраические дополнения первой строки! Такое произведение равно нулю!

И т. д. В итоге, только на главной диагонали останутся ненулевые члены - они равны единице. Теорема доказана.

Эта теорема нам даёт правило нахождения обратной матрицы. Надо составить вспомогательную матрицу, состоящую из алгебраических дополнений, транспонировать её и умножить на число .

Очевидные следствия из определения обратной матрицы:

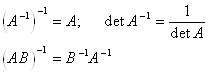
Действительно:

Т. е. матрица АВ - обратная для матрицы В-1А-1.

< Предыдущая		Следующая >