08. Общая теория кривых второго порядка
Удобно будет рассматривать уравнение кривой второго порядка
В следующем виде:
![]() (1)
(1)
Сформулируем признаки, позволяющие узнать тип линии по ее уравнению (1).
Введем некоторые определения.
Группу слагаемых a11x2+2а21xy+а22у2 назовем Группой старших членов. Группу слагаемых 2а13х+2а23у+а33 Назовем линейной частью Уравнения (1).
Коэффициенты а11, a12, а22 назовем Коэффициентами группы старших членов Или старшими коэффициентами, а коэффициенты а13, а23, а33 — Коэффициентами линейной части Или Линейными коэффициентами. Отметим, что коэффициент а33 также называется Свободным членом уравнения (1).
Осуществим параллельный перенос системы координат ОХY в точку 0'(х0,у0), Тогда, как известно, х=х'+х0, у=у'+у0 и в новой системе координат уравнение (1) примет вид:
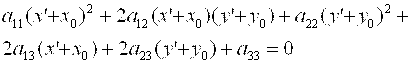
Обозначим коэффициенты при степенях неизвестных в уравнении (*) следующим образом:
 (2)
(2)
Тогда уравнение (*) примет вид:
![]() (3)
(3)
Вывод: при параллельном переносе системы координат, коэффициенты группы старших членов не изменяются, а коэффициенты линейной части изменяются по формулам (2).
Применим формулы поворота системы ОХУ на угол φ т. е.
Х=х'соsφ-y'sinφ;
Y=x'sinφ+y'cosφ;
Получим:
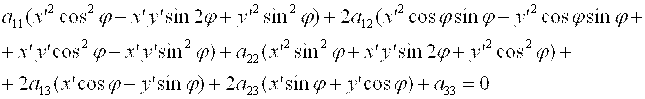
Тогда в новой системе координат, уравнение (1) примет вид:
![]()
Где
![]()
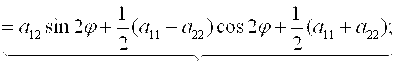
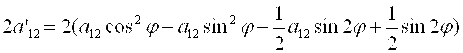 , т. е.
, т. е.
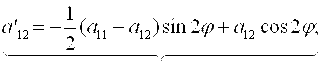
![]()
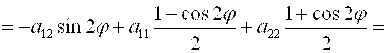
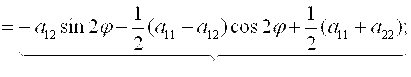
A'13=a13cosφ+a23cosφ
a'23=a23cosφ-a13sinφ (4)
A'33=a33
Вывод: старшие коэффициенты а'11, а'12 и а'22 , выражаются только через угол φ старшие коэффициенты а11, а12 и а22. Коэффициенты а'13 и а'23 выражаются только через угол φ и коэффициенты а13, а23. Коэффициенты а'33 и а33 равны.
Для упрощения равенств (4) введем следующие обозначения:
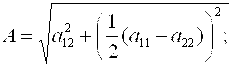
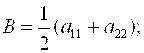
![]() .
.
Тогда
 ,
,
Если А![]() 0 . Введем угол α, где
0 . Введем угол α, где
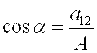 ,
, 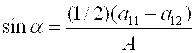
Если же А = 0, то α = 0 и в этом случае a12=(1/2)(а11—а22).
Введем также угол β, считая
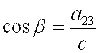 ,
, 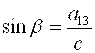 ,
,
Если С![]() 0 . Если же С=0, т. е. а13=а23=0, то β=0 .
0 . Если же С=0, т. е. а13=а23=0, то β=0 .
Тогда выражения (1.30) перепишутся в виде:
a'11=Аsin(2φ+α)+В; а'12=Асоs(2φ+α);
a'22=—Аsin(2φ+α)+В; a'13=Csin(φ+β); (5)
A'23= Ссоs(φ+β); а'33=а33.
Отметим, что величины А, В, С и углы α, β не зависят от φ.
| < Предыдущая | Следующая > |
|---|