07. Классификация кривых второго порядка (КВП)
Уравнение вида
AX2+BХу+СУ2+DX+ЕУ+F=0, (1)
Где A²+ B²+ C² ≠ 0 , называется уравнением кривой второго порядка в прямоугольной системе координат OXY. Преобразуем систему координат таким образом, чтобы уравнение (1) приняло наиболее простой вид.
1. Если в уравнении коэффициент B ≠ 0, то можно повернуть систему координат OXY на угол α такой, что в новой системе координат O’X’Y’ уравнение (1) не будет содержать член с произведением X’Y’.
Действительно, согласно формулам поворота x = x’cosα – y’sinα, y = y’sinα + y’cosα.. Подставляя значения X и Y В (1) легко подсчитать, что коэффициент при X’Y’ примет вид
-2ACosα sinα + B²cos²α - B²sin²α + 2CSinα cosα.
Упрощая, получаем
-ASin2α + BCos2α + CSin2α = 0,
(A - C)sin2α = BCos2α, т. е.
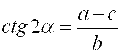 ,
,
Таким образом, в дальнейшем предполагаем, что уравнение КВП имеет вид
AX2+BХу+СУ2+DX+ЕУ+F=0. (2)
2. Если в уравнении (2) А ≠ 0 и D ≠ 0, либо с ≠ 0 и Е ≠ 0, то, осуществляя параллельный перенос системы координат ОХУ, получаем уравнение КВП, не содержащее член с Х, соответственно У.
Действительно, пусть А ≠ 0, D ≠ 0. Выделим полный квадрат при переменной Х в (2).

Применим формулы параллельного переноса
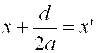 ,
, ![]() ,
, 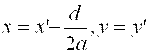
Тогда уравнение примет вид
![]()
Где ![]() . Если же С ≠ 0 и Е ≠ 0, то аналогичным образом исключаем в полученном уравнении член с У.
. Если же С ≠ 0 и Е ≠ 0, то аналогичным образом исключаем в полученном уравнении член с У.
Итак, можно считать, что КВП представляется одним из трёх видов уравнений:
Ах² + By² + C = 0;
Ах² + By + C = 0;
АY² + BХ + C = 0.
Рассмотрим случаи:
1) С ≠ 0. Тогда
Если – (А/с) › 0 и – (B/C) › 0, то это уравнение эллипса.
Если – (A/C) ‹ 0 b – (B/C) ‹ 0, то получаем пустое множество точек на плоскости.
Если – (A/C) › 0 и – (B/C) ‹ 0, то уравнение гиперболы.
Аналогичным образом получим гиперболу, вытянутую вдоль оси ОУ.
2) С = 0. Тогда Ах² + By² = 0;
Если A и B – разных знаков, то всегда можно считать, что А › 0,
B ‹ 0.
Уравнение будет задавать две пересекающиеся прямые Ax ![]() By = 0
By = 0
Если же a и b одного знака, то уравнению удовлетворяет единственная точка О (0,0).
Вывод: любая кривая второго порядка является эллипсом, гиперболой, параболой, парой пересекающихся прямых, парой параллельных прямых, прямой, точкой или пустым множеством.
Укажем еще один способ классификации КВП.
| < Предыдущая | Следующая > |
|---|