06. Полярное уравнение эллипса, гиперболы, параболы

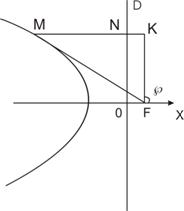
Выведем полярное уравнение для отличного от окружности эллипса, параболы или правой ветви гиперболы. Для этого совместим полюс полярной системы координат с левым фокусом эллипса (правым фокусом гиперболы) или единственным фокусом параболы, а полярную ось направим перпендикулярно директрисе d, соответствующей фокусу. Обозначим через F, р и ε соответственно фокус, фокальный параметр и эксцентриситет кривой. Пусть М — произвольная точка кривой, МF = R— полярный радиус точки М, φ — ее полярный угол. Тогда

─ Полярное уравнение эллипса, отличного от окружности, параболы, правой ветви гиперболы.

Для левой ветви гиперболы

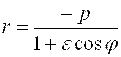
─ Полярное уравнение левой ветви гиперболы.

< Предыдущая		Следующая >