09. Инварианты кривой второго порядка
Инвариантом уравнения (1) относительно преобразования системы координат ОХУ называется такая функция
F(а11, а12, a22, a13, а23, а33),
Которая не меняется при переходе к новой системе координат 0'Х'У'. Таким образом, если f — инвариант, то f(a11,...а33) = f(a'11...а'33).
Теорема. Величины
![]()
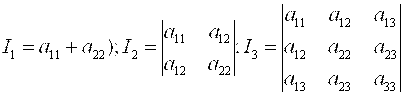 (6)
(6)
Являются инвариантами уравнения (1) линии второго порядка
Относительно преобразований декартовой системы координат.
Доказательство проведем вначале для преобразования параллельного переноса, а затем для преобразования поворота.
Инвариантность I1 и I2 следует из формул (2). Заметим, что из этих формул также следует, что
![]()
 (7)
(7)
Тогда в новой системе координат O’X’Y’

Вычтем из 3-ей строки 1-ю, умноженную на x0, и затем вторую,
Умноженную на у0. Тогда

Теперь из 3-ro столбца вычтем 1-й, умноженный на x0 и второй, умноженный на y0. Получим, что I'3=I3.
Рассмотрим теперь преобразование поворота
![]()

Разложим I'3 по элементам 3-го столбца. Получим:
 =
=
 (8)
(8)
Распишем каждое из 3-х слагаемых в выражении (1.34), пользуясь формулами (1.31).
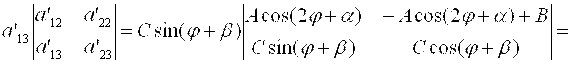
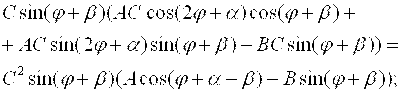 (9)
(9)
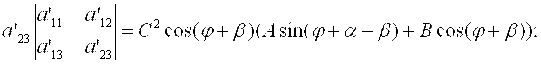 (10)
(10)
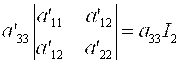 (11)
(11)
Следовательно, из (8) следует, что
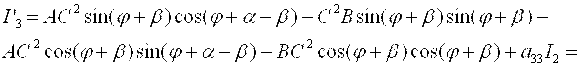
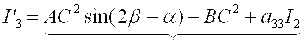 (12)
(12)
Величины А, В, С, углы α, β и I2 не зависят от угла φ. Значит, при любом повороте системы координат, выражение в правой части (12) не изменяется. С другой стороны, при φ=О, I'3=I3. Это и доказывает инвариантность I3. Теорема доказана.
Определим теперь тип линии в зависимости от знаков инвариантов I1, I2 и I3.
Будем говорить, что
при I2>О, уравнение (1) задает Линию эллиптического типа;
при I2<О, уравнение (1) задает Линии гиперболического типа;
при I2=О, уравнение (1) задает Линии параболического типа.
При параллельном переносе можно попытаться добиться того,
Чтобы в уравнении (3) отсутствовали члены 2а'13х' и 2а'23y'. Из формул (2) следует, что это возможно только в том случае, если система
 (13)
(13)
Имеет решение.
Уравнения (13) называются уравнениями Центра линии второго порядка. Если х0, у0 — решение (13), то точка 0'(х0,у0) — Центр линии. Если линия имеет центр, то в результате параллельного переноса начала системы координат в точку 0'(х0,у0) уравнение линии примет вид
![]() (14)
(14)
Поэтому, если точка М(х',у') удовлетворяет уравнению (14), то и точка М'(—х',—у') также удовлетворяет уравнению (14). Таким образом, центр линии является ее центром симметрии.
Заметим, что если кривая второго порядка имеет центр, то, в силу инвариантности I3, получаем
 .
.
Значит,
![]() (15)
(15)
Как было показано ранее, можно повернуть систему координат ОXY таким образом, чтобы уравнение (3) не содержало
Члена 2а'12х'у'. Ясно, что в этом случае а'12=0 и из формул (4) следует, что
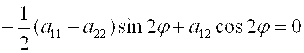
Следовательно, при а12![]() 0
0
 (16)
(16)
Именно при таком выборе угла поворота, уравнение (3) принимает вид:
![]() (17)
(17)
Вывод: Путем параллельного переноса приводим уравнение кривой к виду (14)
![]()
Путем поворота, если а12![]() О, приводим уравнение (14) к виду:
О, приводим уравнение (14) к виду:
![]() (17)
(17)
В системе координат О"Х"У".
| < Предыдущая | Следующая > |
|---|