16. Статистические распределения
Если случайным событием при испытаниях по исследованию признака или свойства процесса является получение Численных значений этого признака, то говорят о наборе случайных величин (СВ), так как каждое число из набора возможных значений может появиться, а может не появиться в результате проведенного эксперимента. Если СВ принимает любые значения на числовой оси или в заданном условиями интервале, то говорят о Непрерывной случайной величине, если же значения определенные, то есть заданы ограничения, то СВ – дискретна. Рассмотрим примеры задания случайных величин.
1. Числа от 1 до 6, нанесенные на гранях куба (гексаэдра) являются примером дискретной случайной величины, если куб использовать в качестве игральной кости (рис.4.1 представляет развертку куба на плоскости).
2. При игре в «Дарс» дискретные величины – это цифры на мишени, фиксируемые случайным образом при бросании «пера» (рис.4.2).Если же на мишени стереть все границы полей, то координаты (x, y) точки А – конца застрявшего пера, будут непрерывными СВ (рис.4.3, т. А).
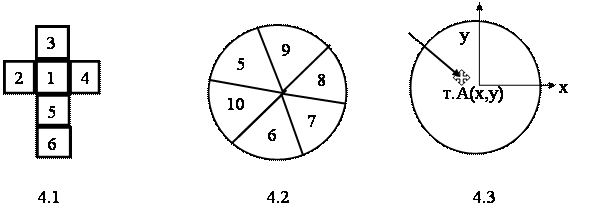
Рис. 4. Примеры случайных величин
Если для каждого значения СВ удается найти соответствующую вероятность, то совокупность этих значений и соответствующих им вероятностей называют Распределением вероятностей. В этом случае распределение можно представить в виде таблицы (табл.6).
Таблица 6
Распределение для СВ
Распределение общего вида на грани куба
СВ X x1 x2 x3 …….xi… xi 1 2 3 4 5 6
Вероятность р р1 р2 р3 …….рi… рi 1/6 1/6 1/6 1/6 1/6 1/6
Очевидно, что для непрерывной СВ вероятность появления ее точного значения всегда равна нулю, так как она вычисляется отношением нулевых размеров точки к размерам площади не равной нулю. Поэтому имеет смысл сравнивать размеры хотя бы малой площади или интервала Δx к размерам площади или к размерам оси, соответствующим полной группе событий. Если обозначить Δр – вероятность попадания случайной величины X в интервал ее значений ΔX, то можно рассчитать вероятность, соответствующую Единичному интервалу значений СВ, т. е. вычислить отношение Δр/ΔX. По смыслу, данное отношение является Плотностью вероятности, которую обозначим символом функции F(X). Наконец, для детального описания необходимо приблизить границы интервала ΔX к точке X. При этом, размеры интервала станут бесконечно малыми, но и соответствующая вероятность попадания СВ в этот интервал станет меньше. Тогда можно найти предел отношения Δр/ΔX при ΔX → 0, и если такой предел существует, то по смыслу он будет характеризовать плотность вероятности, но уже в точке X, принадлежащей бесконечно малому интервалу Dx, что кратко запишем следующим образом:
.
С другой стороны, если этот предел существует, то, как было определено в §6, он называется Производной и обозначается Dp/Dx, то есть F(X) = Dp/Dx. При такой записи каждому бесконечно малому интервалу Dx можно поставить в соответствие величину Dp – вероятность попадания СВ в этот интервал: Dp = F(X)Dx. Поэтому функцию F(X) также называют распределением, точнее, дифференциальной функцией распределения вероятностей, но по смыслу плотность вероятности F(X), как и выше, характеризует вероятность появления случайной величины в единичном интервале ее значений.
Для небольших интервалов Δx можно считать, что F(X) практически не меняется на этом интервале и можно записать: Δр = F(X)Δx. Пример, изображенный на рис.6 демонстрирует результат построения распределения F(X), где случайной величиной X является координата точки мишени, а вероятность Δр определяется экспериментально частотой, т. е. количеством точек с координатами, попадающими в ΔX Случайным образом.
 |
Рис.6. Построение распределения
Из рисунка видно, что вероятность Δр=F(X)Δx численно равна площади заштрихованного столбика и это можно отнести не только к интервалу ΔX, но и к любому другому интервалу значений СВ, используя теорему сложения вероятностей для несовместных событий. Если ступеньки станут очень частыми, т. е. когда в пределе ΔX можно заменить на Dx, экспериментальная диаграмма перейдет в график идеальной функции плотности вероятности, как это представлено на рис.6 (справа). Среди многих функций плотности вероятности распределение, изображенное на рис.6 встречается очень часто и аналитически график этой функции записывается в виде:
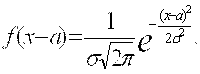
Данная функция исследована в рамках математики Гауссом, носит его имя и называется в теории вероятностей Нормальным распределением. Входящие в него величины A и σ являются параметрами распределения, а π и Е – иррациональные числа.
Рассмотрим полученное распределение вероятностей и выясним его основные характеристики (рис.7).
 |
Рис.7. Нормальное распределение
Так как у плотности вероятности F(X) есть максимум, то соответствующее этому максимуму наиболее вероятное значение СВ называют Модой.
Так как функция F(X) симметрична, то очевидно, что вычисление среднего значения X (обозначается 
, Xср или <x>) совпадает c линией симметрии.
Если в нормальном распределении сделать замену переменных и ввести новую величину T=(X-A)/σ, т. е. из каждого значения случайной величины X вычесть А, то получится функция
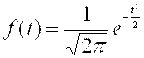, смещенная в начало координат, так как теперь ее максимум будет совпадать с началом координат (при T=0). Но максимум функции F(T) совпадет с максимумом F(X), только если А = 0. Это означает, что величина А характеризует положение центра симметрии, т. е. вместе с этой величиной меняется и среднее значение СВ. Поэтому XСр = а.
Функция F(T) отличается от F(X) еще и тем, что параметр σ принял значение равное 1. Поэтому, если в распределении F(X) величина σ будет больше 1, то в максимуме функции (при X = A) коэффициент перед экспонентой е уменьшится и график в точке X = A пройдет ниже, чем при σ = 1. Этот факт будет означать, что доля значений СВ близких к Хср уменьшилась и, следовательно, увеличилась доля значений СВ далеких от Х = а. В этих интервалах график F(X) пройдет (см. рис.7) выше исходного графика (с σ = 1). В результате, разброс СВ от среднего значения возрастет. Поэтому величина σ является Мерой разброса или среднеквадратичным отклонением случайной величины от ее среднего значения и называется также Стандартным отклонением. Так как в показателе степени функции Гаусса фигурирует σ2 , то и эта величина является параметром распределения и называется дисперсией (D). Можно записать, что σ = 
.
Теперь научимся рассчитывать средние характеристики распределений. Начнем с простого примера. Для того, чтобы вычислить среднее значение СВ, появляющейся в результате бросания игральной кости в форме кубика, очевидно, необходимо просуммировать числа, нанесенные на гранях и разделить на общее число граней. Тогда имеем:
и, учитывая, что Х1 =1, Х2=2,…, Х6 = 6, а Р1 = 1/6, Р2 = 1/6, …, Р6 = 1/6, можно записать формулу для вычисления среднего значения (его называют Математическим ожиданием СВ):
,
где i – индекс суммирования по всем значениям СВ.
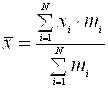
Если количество случайных событий равно 
, вероятность появления каждого из них определяется как РI = Mi/N, а общее число событий равно 
, то среднее значение СВ 
, или, окончательно имеем:
.
Если теперь на гранях кубика вместо каждого значения СВ запишем величину, возведенную в квадрат, то для среднего значения новой случайной величины получим:
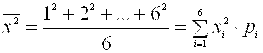, или в общем случае, имеем:
.
Получили формулу для вычисления среднего значения квадрата случайной величины. Рассуждая аналогичным образом, можно вычислить и дисперсию случайной величины, как ее среднеквадратичное отклонение от среднего значения. В этом случае имеем:
Далее, можно вычислить среднекубическое отклонение СВ и среднее значение четвертой степени отклонения от Хср:
, 
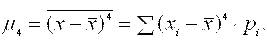
Для непрерывных случайных величин формулы средних значений трансформируем следующим образом:
· вместо Xi записываем текущую координату Х;
· вместо вероятности рI Записываем Dp=F(X)Dx, т. е. вероятность попадания в бесконечно малый интервал Dx значений СВ;
· вместо суммы 
Вводим сумму бесконечно малых величин 
, которая, как известно, называется интегралом.
В результате имеем еще один набор формул для вычисления средних значений случайной непрерывной величины.
;
;
;
;
.
Для нормального распределения Хср= а, D =σ2 , μ3=0, μ4=3. Для других распределений величину μ3/σ3=As называют коэффициентом ассимметрии и этот коэффициент тем больше, чем значительнее нарушена симметрия распределения по сравнению с нормальным. Величину, равную μ4/σ4 –3=Эк называют эксцессом. Эта величина также характеризует нарушение формы кривой («островершинность» или «плосковершинность») по сравнению с нормальным распределением.
При переходе от теоретически рассчитанных вероятностей к частотам, получаемым в эксперименте, важно понять различие между «частотной» плотности вероятности f(x)=Δp/Δx и функцией плотности F(X)=Dp/Dx. В первом случае, вероятность Δp=F(X)Δx геометрически соответствует размерам площади под графиком (см. рис.6), опирающейся на интервал Δx, а во втором, размеры этой площади бесконечно малы. Так как СВ может попасть или в один интервал Δх1 , или в соседний –Δх2 , или…и т. д., то для поиска вероятности попадания величины Х в относительно большой интервал (от А до В на рис.6), необходимо воспользоваться теоремой сложения вероятностей для несовместных событий (если считать, что СВ не может попасть сразу в несколько интервалов). Сложение же бесконечно малых Dp, как мы уже говорили ранее, требует умения решать интегралы от функции распределения в заданных пределах. С другой стороны, оценка величины соответствующей вероятности может быть сделана, как в теоретическом, так и в эмпирическом распределении, по размерам площади «столбиков», опирающихся на интервал от А до В (рис.6). Отдельные этапы построения распределений можно понять, анализируя таблицы 3.4, 5.1, 5.2, 5.3 и соответствующие им графики на рис.5.3 (полигон частот) и рис.5.4 (гистограмма), представленные в Приложении II.
По теореме полной вероятности сумма всех вероятностей (всех площадей) должна характеризовать вероятность достоверного события, т. е. равняться единице, а тогда и интеграл 
=1. (Последнее выражение называют Условием нормировки функции плотности вероятности). Однако, если экспериментальные данные оказались ограниченными между точками ХН - нижней границей экспериментальных данных и ХВ – верхней границей, то и на графике функции F(X) площади, расположенные под графиком слева от нижней границы и справа от верхней в расчетах не участвуют (отброшены). Поэтому вся площадь под кривой распределения уже не соответствует 100% возможностей, а размеры Δх, взятые от т. Н до т. В определяют так называемый Доверительный интервал. Если например, в нормальном распределении доверительный интервал ограничен точками ХН=хср–σ и ХВ=хср + σ, то площадь под графиком составляет 68,3% от всей площади под кривой (соответственно, вероятность Р(–σ<х–хср<+σ)= 0,683). Если ХН=хср– 2σ и ХВ=хср+2σ, то размеры площади «доверия» составляют 95,4%, а при отклонениях Х от Хср равных ±3σ вызывает наибольшее доверие, т. к. соответствующая площадь составляет величину 99,7% от полной площади под кривой распределения.
| < Предыдущая | Следующая > |
|---|
