15. Математические основы статистики

Математическую основу статистики составляет теория вероятностей, исходным понятием которой является Случайное событие. При пространственно – временном описании явлений элементарное событие считается заданным или определенным, если для него известно Место и Момент времени. Такой подход позволяет ввести наглядную геометрическую модель пространства событий либо дискретную (рис.1а), либо непрерывную (рис.1б). В первом случае за конкретное элементарное событие можно условно принять одну из клеток дискретного клеточного пространства, например ту, которая заштрихована на рис.1а. Во втором случае конкретному элементарному событию соответствует одна из точек непрерывной плоскости.

 

 

 

 

 

 

 

Рис.1. Дискретное и непрерывное представление полной группы событий

Понятие элементарности, вообще говоря, относительно, так как пространство дискретных событий, например, можно представить и более мелкими клетками. Тогда в заданном комплексе условий можно оговорить, что существует предел дробления. Сложное событие будем представлять как совокупность (область) элементарных (см. рис.1а, б).

Одинаковые размеры отдельных клеток будут означать, что соответствующие им элементарные события равноправны (равновозможны).

Значительно сложнее разобраться в понимании Случайного, так как «механизм» Неопределенности, лежащий в основе случайного только начинает поддаваться исследованию в рамках естествознания. Со времен древних греков Необходимое и Случайное являлись следствием существования двух состояний Мира: состояние порядка («Космоса») и беспорядка («Хаоса»), причем Хаос признавался первичным. В наше время фундаментальная модель, описывающая исходное хаотическое состояние Мира вселенных Базируется на представлении о физическом «вакууме», богатом Виртуальными, Потенциально возможными структурами, некоторые из которых случайным образом реализуются в виде вселенных при нарушении симметрии однородности физического вакуума. Одна из вселенных – Метагалактика, в которой мы живем, родилась около 14 миллиардов лет назад. Состояние хаоса при развитии Вселенной переходит с одного структурного уровня развития на другой (от элементарных частиц до биологических и социально-экономических форм), и на каждом уровне из хаотического состояния рождаются новые структуры. Поэтому Случайность Также закономерна, как и Необходимость. Математика изучает мир виртуальных структур и остается выяснить, каким образом Возможное («ненаблюдаемое») реализуется как Действительное («наблюдаемое»).

В теории вероятностей Случайным событием называют такое событие, которое может реализоваться (произойти, появиться), а может не реализоваться в заданном комплексе условий. Количественной мерой определенности появления случайного события является Вероятность.

Множество Элементарных (недробимых), Равновозможных (равноправных), Единственно возможных (т. е. кроме них не рассматриваются другие события в данном комплексе условий), и Попарно несовместных событий составляют Полную группу. Последнее требование попарной несовместности необходимо для того, чтобы элементарные события были различимыми. Полная группа может быть составлена из конечного и бесконечного множества элементарных событий, из которых затем можно составлять сложные события, производя определенные операции.

На рис.2 представлен пример наглядного изображения полной группы из N - случайных событий и различные варианты из M-, K-, L- сложных событий, обозначенных заглавными латинскими буквами.

 

 

 

 

 

 

 

 

 

 

 

 

 

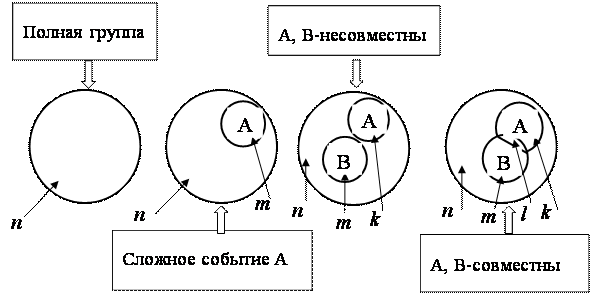Рис.2. Геометрическая интерпретация событий

Очевидно, что чем большую часть среди всех событий составляет сложное событие А, тем меньше неопределенность, то есть более определенным является его появление. Отсюда следует, что вероятность данного события А, которую обозначим P(A), можно измерить этой долей. Тогда следует записать:

.

Рассмотрим несколько примеров на вычисление вероятности.

Пример 1. Пусть при случайном бросании монеты на плоскую твердую поверхность фиксируется сверху либо появление герба, либо обратной стороны («решки»). В этом случае вероятность появления герба, т. е. величина р(Г), по определению вероятности, равна 1/2, так это событие одно из двух.

Пример 2. Пусть при Случайном выходе в течение часа из дома, расположенного вблизи троллейбусной остановки Вы садитесь на первый, пришедший к остановке троллейбус (с номерами 2, 9 или 10). Известно, что интервал времени между появлениями троллейбусов Δt =20 мин. и порядок их следования, обозначенный в скобках, выдерживается точно. Какова вероятность у Вас оказаться в троллейбусе №9? По определению вероятности, нужно найти какую долю интервал Δt составляет по отношению к временному интервалу T = 1часу, включающему в себя все события без повторения. Тогда

Р(№ 9) = р9 = ΔT/T =20/60 = 1/3.

Такой же результат Вы получите и при вычислении вероятностей попадания на троллейбусы №2 и №10. Все события оказываются равновозможными.

Если же на оси времени T интервалы между приходами разных по номеру троллейбусов (рис.3) в течение часа различны, то и ответ получится другой.

 

 

 

 

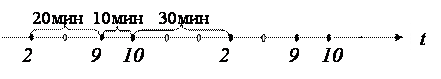Рис.3. К примеру 2.

Действительно, вероятность попасть «на десятку» равна р10 = 1/6, «на двойку» р2 =3/6 =1/2 и «на девятку» р9 =2/6 =1/3, так как N = 6 (общее число временных отрезков, соответствующих 1часу), а M2 =3, M10=1, M9=2, что соответствует временным интервалам, в конце которых появляется троллейбус с соответствующим номером.

Попадание в течение часа на любой из перечисленных троллейбусов является Достоверным событием, так как оно Обязательно происходит в данном комплексе условий. Как вычислить вероятность достоверного события? Учтем, что рассмотренные нами события несовместны, так как Вы не можете одновременно попасть в какие-либо два (тем более три) троллейбуса.

Итак, нам все равно: попасть ли в интервал между №2 и №9 (m9=2) в интервал между №9 и №10 (m10=1) или в интервал между №10 и №2 (m2=3). Тогда произойдет или первое событие, или второе, или событие третье, по времени составляющие сумму отдельных интервалов и вероятность по определению будет равна Р(или№9, или№10, или№2) =(M9+m10+m2)/n =1. Заменим логическую связку “или” на “плюс”(+) и будем считать, что производится Сложение событий. В результате, вероятность достоверного события, как суммы всех событий, оказалась равной 1.

Обобщение полученного результата на два произвольных несовместных события А и В из одной полной группы, приводит к формуле сложения вероятностей:

р(А или В) = р(А+В) = р(А) + р(В).

Используя диаграмму на рис.2 для двух несовместных события А, В, рассуждая аналогично, получаем такой же результат:

р(А или В) = р(А+В) = (M + K)/N = M/N + K/N = р(А) + р(В), Т. е. складываем площади M и K и делим на общую площадь N.

Если события А и В совместны (рис.2), то есть когда соответствующие площади пересекаются, имеем:

Р(А Или В) = (M + K – L)/N = M/N + K/N – L/N, где при сложении площадей M и K площадь L участвует два раза и поэтому один раз ее необходимо вычесть.

Площадь L характеризует сложное событие, заключающееся в том, что происходит совместно и А и В. Тогда, Р(И А, И В) = L/N, а соответствующее сложное событие называют произведением А и В и обозначают знаком обычного произведения, т. е. Р(АВ) = L/N. Как выразить эту вероятность через вероятности событий А и В? Для этого запишем следующее выражение:

Р(АВ) = L/N = (L/M)(M/N), либо Р(АВ) = L/N = (L/K)(K/N). Величина L/M характеризует вероятность события В при условии, что за полную группу выбраны элементарные события, соответствующие А (то есть считается, что событие А произошло и нам «известны» все M элементарных события). В этом случае, величину L/M называют Условной вероятностью события В или вероятностью события В, вычисленную при условии, что А произошло. Обозначим условную вероятность РА(В) = L/M. Тогда, соответственно имеем: L/K = рВ(А) и формула умножения вероятностей запишется следующим образом:

Р(АВ) = р(А)рА(В) = р(В)рВ(А).

Пример 3. Пусть мы имеем один экземпляр кассы из 33 букв русского алфавита. Рассчитаем вероятность того, что при случайном вытаскивании букв из кассы на столе можно будет выложить слово «УМ».

Очевидно, что появление буквы У на первом месте определится вероятностью Р(У) = 1/33 (по определению вероятности). Вероятность появления буквы М на втором месте, вычисленная при условии, что уже произошло появление буквы У, будет равна РУ(М) = 1/32, а не 1/33, как если бы мы вычисляли безусловную вероятность события М. Тогда Р(УиМ) = Р(УМ) =р(У)рУ(М) = (1/33)(1/32) ≈ 0,001.

Если нас интересует, с какой вероятностью эти же буквы появятся в любом порядке, а нужное слово мы выложим сами, то это уже другая задача. Интересующее нас событие может быть записано в скобках при вычислении вероятности следующим образом:

р[(УиМ) Или (МИУ)] = р(УМ + МУ) = р(УМ) + р(МУ) ≈ 0,001 + 0,001= 0,002. Вероятности Р(УМ) и Р(МУ) вычисляются одинаково, а поэтому равны.

При решении задач может оказаться, что РА(В) = р(В), т. е. L/M = K/N. Это означает, что вероятность события В не меняется от того, что произошло или не произошло событие А. Такое отношение между событиями В и А логично назвать термином Независимость В от А. Можно доказать (легко это сделать самостоятельно в качестве упражнения), что если В не зависит от А, то и А не зависит от В. Для независимых событий формула умножения вероятностей будет выглядеть следующим образом:

р(АВ) = р(А)р(В).

Сведем полученные результаты в одну таблицу (табл.5).

Таблица 5

СЛОЖЕНИЕ УМНОЖЕНИЕ

Р(А + В) = р(А) + р(В) – р(АВ) Р(АВ) = р(А)рА(В) = р(В)рВ(А)

(события совместны) (события зависимы)

Р(А + В) = р(А) + р(В) Р(АВ) = р(А)р(В)

(события несовместны) (события независимы)

(формула полной вероятности).

Если теперь начать практическую проверку теоретически вычисленных вероятностей, то вполне возможно, что ожидаемая доля события А не будет соответствовать реальной частоте появления этого события. Пусть например, при бросании монеты из N =10 испытаний герб появился только M = 3 раза. Тогда относительная частота (частость) появления этого события составляет величину M/N = 3/10, что значительно отличается от 1/2. Даже если увеличить число испытаний до 100, 1000, 10000 и т. д., то и в этом случае точное значение частости, равное 1/2 может и не реализоваться, но при дальнейшем увеличении N или, как говорят, в пределе значение частости будет отклоняться от 1/2 все меньше и меньше, т. е. в пределе, относительная частота события А стремится к величине вероятности, вычисленной из знания полной группы. Кратко этот вывод записываем следующим образом:

.

Запись означает, что для экспериментального нахождения вероятности события необходимо обнаружить Тенденцию стремления частостей к определенной величине (предел частоты). Графически, рассмотренный пример будет выглядеть так, как это изображено на рис.3, (повторение рис.13 из §5, Часть I).

 

 

 

 

 

 

 

 

 

 

Рис. 3. К частотному определению вероятностей

< Предыдущая		Следующая >