11.5. Найти неопределенный интеграл
Перед решением задач этого раздела необходимо внимательно изучить Свойства интегралов, а при решении иметь перед собой список Табличных интегралов от элементарных функций. Информация по свойствам и решению табличных интегралов дается в Приложении к данной методической разработке.
Все основные методы решения интегральных задач основаны на поиске такого приема, который позволяет свести исходный интеграл к табличному или сумме табличных интегралов. Сюда относится: (1) – Разложение подинтегральной функции на сумму более простых, которые легче свести к табличным; (2) – Замена переменных, приводящая интеграл к табличному; (3) – интегрирование функции По частям. Во всех случаях следует, по возможности, упрощать вид подинтегральной функции. Рассмотрим применение методов решения интегралов, то есть поиска «первообразной» функции на конкретных примерах.
(1): 
Применен метод разложения подинтегрального выражения.
(2):  .
.
Упрощение подинтегральной функции привело к табличному интегралу.
(3):
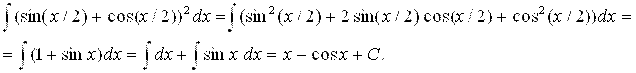
Использовано упрощение и разложение подинтегральной функции.
(4):

После подстановки в подинтегральное выражение рассчитанных величин, получим:
 .
.
(5): 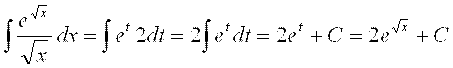 .
.
При решении произведена замена переменных:
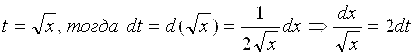 . Полученное выражение и было подставлено под интеграл.
. Полученное выражение и было подставлено под интеграл.
(6): Найти ![]() .
.
Для решения обозначим X = U, а v = Sin X. Тогда DV = Cosx Dx , а dx = dv. Исходный интеграл будет выглядеть следующим образом:
![]() . Применен метод решения по частям. Из этого примера видно, что интегрирование по частям применяется в том случае, когда подинтегральная функция представляет собой Произведение двух функций.
. Применен метод решения по частям. Из этого примера видно, что интегрирование по частям применяется в том случае, когда подинтегральная функция представляет собой Произведение двух функций.
(7): Найти 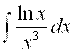 .
.
Введем функцию U = X-2, для которой -2X-3Dx = Du. Отсюда, стоящее под интегралом выражение Dx/X3 можно заменить на - Du/2. Обозначая Ln X = v, получим подинтегральное выражение в форме, к которой применим метод интегрирования по частям:
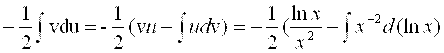 .
.
Величина D(Ln X) = Dx/X и после ее подстановки под интеграл, получим:
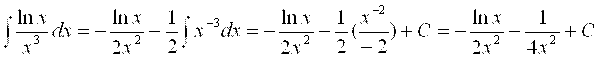 .
.
| < Предыдущая | Следующая > |
|---|