11.4. Вычисление производных

Для решения задач на вычисление производных необходимо Иметь Справочный материал по результатам таких вычислений для простейших функций (см. Приложение), Знать Основные правила вычислений от Произведения функций, от Отношения функций, от Степенных функций и от Сложных функций. Основные правила взятия производных также представлены в Приложении.

Рассмотрим несколько типовых примеров вычисления производных от функций, которые могут встретится при выполнении контрольной работы.

(1): У = exsin x. y’ = (ex)’sin x + (sin x)’ex = exsin x + excos x = ex(sin x + cos x).

Использовалось правило дифференцирования произведения двух функций.

(2): 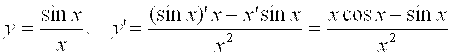. Использовано правило дифференцирования отношения двух функций.

(3): у = 5х4 – 3х2 +2х – 1. у’ = 5∙4x3 – 3∙2x + 2 = 20x3 – 6x + 2. Использовано правило дифференцирования суммы степенных функций.

(4): У = Ln |Sin X|,X≠ 2Kπ .Обозначим U = Sin X.Тогда Y = Ln U(X).у’=(Ln U)’ = 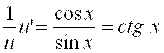. Использовалось правило дифференцирования

Сложной функции.

(5):

(6): У = хх . Прологарифмируем обе части равенства: Ln Y = Xln X. Теперь возьмем производные от обеих частей: (Ln Y)’ = X’Ln X + X(Ln X)’, откуда следует:

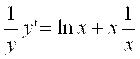. Из полученного равенства выражаем производную У’:

У’ = Y(Ln X + 1) = Xx(Ln X + 1).

(7): У = ах. Применяя к заданной функции тот же подход, что и в предыдущей задаче, получаем: Ln Y = Xln A, (Ln Y)’ = Ln A, Y’/Y = Ln A, Y’ = = AXln A.

< Предыдущая		Следующая >