11.3. Найти пределы функций
Этого вида задачи решаются несколькими различными приемами.
(1). Сведением пределов заданных функций к двум «замечательным» пределам, для которых известен результат расчета. Первый замечательный предел имеет следующий вид: 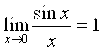 , а Второй записывается так:
, а Второй записывается так:  . Иногда считают, что второй предел является определением числа е – основания натуральных логарифмов. Второй замечательный предел после замены переменного у = 1/х можно представить в другой форме, которая также используется при решении задач:
. Иногда считают, что второй предел является определением числа е – основания натуральных логарифмов. Второй замечательный предел после замены переменного у = 1/х можно представить в другой форме, которая также используется при решении задач:  .
.
(2). Функция, предел которой следует определить, часто представляет собой отношение двух степенных функций общего вида (двух многочленов). Эти отношения после подстановки в них значения бесконечного предела, к которому стремится аргумент (Х → ∞) представляют собой неопределенности вида ![]() .
.
Можно показать, что такие задачи решаются Делением числителя и знаменателя на ХK, где k – наибольший показатель степени в многочленах.
(3). Если аргумент стремится к какому – либо конечному пределу, то необходимо подобрать такую Замену переменных, чтобы изменить соотношение величин показателей степени многочленов в числителе и знаменателе.
(4). Наконец, для раскрытия неопределенности вида [∞ – ∞] используется прием умножения разности функций (F – U) на Сопряженное Выражение: (F + U).
(5). Иногда, при поиске предела отношения двух произвольных функций используется прием разложения функций в соответствующие степенные ряды. Полезно также применять, так называемое, Правило Лопиталя: предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных.
Рассмотрим несколько конкретных примеров на вычисление пределов. При решении задач необходимо Знать операции, которые можно производить с пределами (см. Приложение I).
(1): ![]() .
.
 .
.
(2): .
.
(3): 
(4): 
(5):  .
.
Первый шаг применения правила Лопиталя не привел к разрешению
неопределенности. Применим это правило к полученному пределу еще раз:
 .
. ![]()
| < Предыдущая | Следующая > |
|---|