11.2. Построение графиков функций

1). Y = Ax + B. Решение. Так как Функция линейна, то для ее построения достаточно задать две точки. Для удобства вычислений координаты первой точки определим, положив Х1 = 0. Тогда У1 = B и на графике появится точка А (0, B). Для второй точки В удобно положить У2 = 0. В этом случае Ах2 = – B, откуда имеем: Х2 = – B/A. Координаты этой точки, таким образом, будут равны : В (– B/A, 0). Для построения графика выбираем оси координат, например, так, как это показано на рис. 2. На этом же рисунке начертим графики заданной функции при различных по знаку величинах А и B, то есть при А > 0 и b > 0 (линия 1); при А > 0 и B < 0 (линия 2); при А < 0 и B > 0 (линия 3); при А < 0 и B < 0 (линия 4).

При построении графика знаки величин А и B вынесены, поэтому сами числа положительны. При B = 0 линия 1 и линия 2 совпадут, направления их не изменятся, а график пройдет через точку (0,0), то есть через начало координат (пунктирные линии).

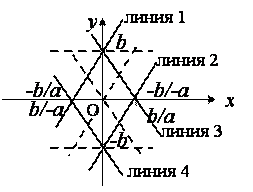
Рис. 2. Графики линейных функций

То же самое произойдет с линиями 3 и 4. При А = 0, У = B = Const и прямые пройдут параллельно оси Ох через точки ± B (пунктирные линии).

2). Следующий способ построения графика рассмотрим на примере Показательной функции. В основу положим методику построения по точкам, то есть использование таблицы значений аргумента х и функции У = F(х).

Пусть F(х) = 2х . Для построения графика составим Таблицу 1:

	Х	-4	-3	-2	-1	0	1	2	3	4	5	6	7
	F(х)	1/16 (0,06)	1/8 (0,125)	1/4 (0,25)	1/2 (0,5)	1	2	4	8	16	32	64	128

Рис. 3 Построение графика функции Y = 2х по точкам

Вид графика легче всего представить в простейшей форме, используя стандартную программу Excel, введением в ячейки программы нижнюю строку значений функции из Табл. 1. (Обозначение осей координат и их расположение требует некоторого дополнительного умения работы с программой Excel).

Если таким же способом строить график функции F(х) = 2-х , то в Табл,1 положительные и отрицательные значения аргумента х поменяются местами. Вводить эти новые данные для совместного построения двух показательных функций: У = 2х и У = 2-х следует в обратном порядке – от большего значения к меньшему (справа – налево). В результате получаем на диаграмме (Рис. 4) общий вид графиков исследуемых показательных функций, где Ряд1 соответствует функции У = 2х, а Ряд2 – функции У = 2-х.

X

Y(x)

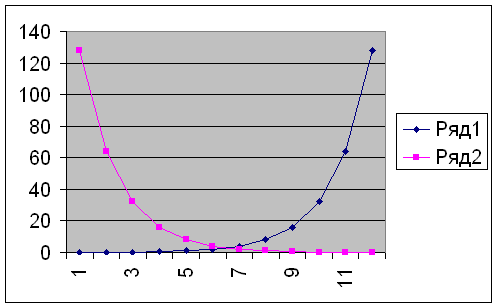
Рис. 4 Построение графиков функций y = 2х и y = 2-х по точкам

Аналогичный результат можно получить и при построении графика на миллиметровой бумаге «от руки».

Таким же образом, составляя таблицу значений аргумента и соответствующих значений функции, строятся все основные математические функции:

· квадратичная: У = ах2 + вх + с;

· степенная: У = аNXn + A(N-1)X(N-1) + ….+ A2X2 + Ax + A0 при N – целом и дробном, когда У = ха/в = , положительном и отрицательном, когда У = х-N = 1/Xn;

· экспоненциальная: у = е±х, где е – иррациональное число, приблизительно равное 2,718281828459…, которое часто встречается при описании природных и социальных процессов (в области статистики, экономики, психологии, социологии);

· логарифмическая: У = Logax и, в частном случае У = Log10X = Lg X, а также, У = LogЕX = Ln X ;

· тригонометрические: sin x, cos x, tg x, ctg x.

Почти все эти функции хорошо известны из школьного курса математики, а способы их построения достаточно подробно изложены в рекомендуемой литературе. Математические операции, которые можно производить с показательными и логарифмическими функциями, представлены в Приложении к данным методическим рекомендациям.

< Предыдущая		Следующая >