11.6. Вычисление определенных интегралов

Методы вычисления определенных интегралов основываются на поиске первообразной функции, как это делается в случае решения задач с неопределенными интегралами, и последующим применением формулы подстановки пределов интегрирования, называемой Формулой Ньютона – Лейбница: .

Рассмотрим несколько примеров применения этой формулы.

(1): .

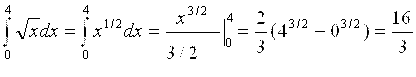(2): .

В этом примере использовано решение по частям неопределенного интеграла, заданного в примере (7) предыдущего раздела.

Часто (например, при обработке статистических данных) вычисление определенного интеграла бывает связано с поиском площади фигуры, ограниченной известными функциями. Рассмотрим один такой пример.

(3):Вычислить площадь фигуры, ограниченной линиями: X=, Х = 0, У =

Данные этой задачи представим графически (рис. 5).

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 5. К задаче (3)

Из рисунка видно, что площадь S = S0ABC – S0BC . Для вычисления площади прямоугольника 0АВС необходимо знать координаты точек А и В. Прямые у = 4 и х = 0 , на пересечении которых лежит точка А, определяют ее координаты: А(0,4). Координата «у» точки В также определена прямой у = 4, а ее «х» – координата может быть найдена из совместного решения системы уравнений: , так как эта точка находится на пересечении линий, соответствующих этим уравнениям. Простая подстановка верхнего уравнения в нижнее дает х = 2. Тогда точка В имеет координаты В(2,4). Расстояние 0А = 4ед., а расстояние АВ = 2ед., поэтому площадь S0ABC = 8ед.2 Далее, исходя из геометрического смысла определенного интеграла, площадь криволинейного треугольника 0ВС следует искать с помощью интегрирования в пределах от х = 0 до хмакс= 2:

. Окончательный ответ S = 8 – 8/3 = 16/3.

< Предыдущая		Следующая >