05. Пределы и их вычисления
Степенная функция, которая представлена выше (7), может рассматриваться как многочлен, состоящий из суммы некоторой последовательности чисел, образующейся при зафиксированном значении аргумента. Положим X = Q , а коэффициенты An+1 при xn для простоты будем считать одинаковыми и равными A. Функция Y = Sn перепишется в следующем виде: при N = 0, S1 = A1Q0; при N =1, S2 =A1Q0+A2Q;При N=2, S3 = A1Q0+A2Q + A3Q2 и т. д. до Sn = Sn—1+ Anqn-1. Если все коэффициенты равны A, то последовательность будет записана следующим образом: Sn = A(1 + Q + Q2 + Q3 +….+ Qn-1). Выражение, стоящее в скобках замечательно тем, что при делении любого слагаемого из этой суммы на предыдущее слагаемое всегда дает один и тот же результат, равный Q. Такая последовательность называется Геометрической прогрессией. Сумма всех N членов геометрической прогрессии определяется по формуле:
![]()
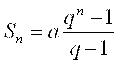 , (Q ≠1) (9)
, (Q ≠1) (9)
((?): Как вывести эту формулу самостоятельно? )
Формула (9) положена в основу расчетов пенсионного фонда при начислении пенсионных накоплений. Если величина A = Р0 определяет неизменный вклад, а Q = 1 + R/100, где R – определенный законом процент годовой добавки, то легко вычислить накопления вкладчика за несколько лет:
Sn = Р0 (1 + q + q2 + q3 + … + qn-1 )= 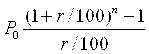 .
.
Очевидно, сумма накоплений будет расти от года к году и в идеальном случае (или говорят, «в пределе») будет расти бесконечно. Математически последняя фраза записывается следующим образом: Sn → ∞ При N → ∞ Или символически так: ![]() .
.
Вообще говоря, при решении вопросов, связвнных с накоплениями, часто решается проблема долгосрочных вкладов. Какое предложение банка является выгодным, существует ли предельная сумма накоплений и т. п. Для решения некоторых типичных задач рассмотрим различные схемы начисления процентов, предлагаемые банками.
1. Простой процент.
При простом проценте к начальному вкладу Р0 добавляется ежегодно одна и та же величина, составляющая R процентов от начального вклада. Таким образом в конце первого года у вкладчика окажется накопленной сумма 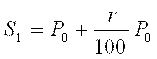 , в конце второго года – сумма
, в конце второго года – сумма
 , а в конце N – го года
, а в конце N – го года
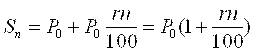 .
.
Если сумму накоплений считать функцией от T – времени сохранения вклада, то полученная зависимость оказывается линейной:
 . Очевидно, что при T → ∞, y → ∞, то есть
. Очевидно, что при T → ∞, y → ∞, то есть ![]() . На графике линейной зависимости суммы накоплений от времени рост накоплений зависит тангенса угла наклона k, то есть от первоначального вклада и от начисляемого процента.
. На графике линейной зависимости суммы накоплений от времени рост накоплений зависит тангенса угла наклона k, то есть от первоначального вклада и от начисляемого процента.
2. Сложный процент.
![]() При начислении сложного процента от вклада P0 накопления за предыдущий год являются начальным вкладом за год вычисляемый. Тогда в конце первого года будем иметь:
При начислении сложного процента от вклада P0 накопления за предыдущий год являются начальным вкладом за год вычисляемый. Тогда в конце первого года будем иметь:
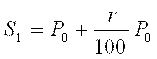 .
.
(?): А есть ли выгода по сравнению с простым процентом?
В конце второго года накопления будут выражены суммой
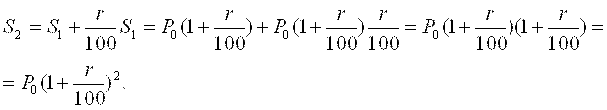 Наконец, за N лет накопится сумма
Наконец, за N лет накопится сумма 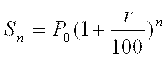 . (10)
. (10)
![]() (?): Сколько лет придется копить определенную сумму Sn в банке, предлагающем R(%) годовых, если первоначальный взнос составляет P0?
(?): Сколько лет придется копить определенную сумму Sn в банке, предлагающем R(%) годовых, если первоначальный взнос составляет P0?
(?): Каков должен быть первоначальный вклад, если за N лет при начислении R(%) годовых нужно накопить сумму Sn?
(?): Какой процент вклада был предложен банком, если клиент за N лет при первоначальном вкладе P0 Получил сумму Sn?
Более сложная задача выбора решения возникает тогда, когда банк предлагает операцию начисления процента производить не ежегодно, а несколько раз в течение года, например предлагает R(%) годовых разбить на кварталы или месяцы. Тогда начисления фактически производятся при проценте RN = R/N , где число N показывет на сколько частей разбит год, а R Попрежнему определяет годовой процент. Понятно, что если банк предлагает годовых ежеквартально, то RN = R4 = R/4, А если ежемесячно, То RN = R12 = R/12. В формуле (10) показатель степени N обозначал не только срок хранения вклада в годах, но и сколько раз производился перерасчет. В первом случае за год эта операция проводилась 4 раза, а во втором 12 раз. Поэтому годовые накопления вкладчика S1 в первом примере будут вычисляться по формуле:
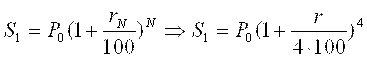 , а во втором примере эта величина составит
, а во втором примере эта величина составит 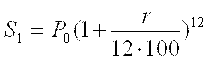 . За несколько лет накопления окажутся равными
. За несколько лет накопления окажутся равными  . (11)
. (11)
Если первый банк предлагает 15,3% годовых ежеквартально, второй 15,2% ежемесячно, имеет смысл вначале произвести расчет, а затем принять наиболее выгодное предложение. Очевидно, что величина чистой прибыли ΔР определится разностью между полученной прибылью S1 (за один год) и вкладом P0 : ΔР = S1 – P0. Но эта разность зависит от начального вклада, а поэтому оценку предложений банков необходимо произвести не в абсолютных, а в относительных величинах, как отношение чистой прибыли к первоначальному вкладу. Тогда следует записать:
 . Если теперь в полученное выражение подставить конкретные данные, то решение будет найдено. В общем виде оно будет выглядеть следующим образом:
. Если теперь в полученное выражение подставить конкретные данные, то решение будет найдено. В общем виде оно будет выглядеть следующим образом:
 . (12)
. (12)
![]()
(?): Чье же все-таки предложение является более выгодным?
(?): Какой способ расчета при одном и том же проценте R является более выгодным для банка: ежеквартальный, ежемесячный или ежедневный?
Наиболее сложным в этой ситуации является Вопрос о предельной выгоде при дроблении годичного интервала на все более мелкие интервалы времени, то есть при стремлении величины N к бесконечности. Если годовой процент выразить в долях, а не в процентах, то есть ввести величину А = R/100 , обозначить N = x, а чистую прибыль (плюс единица) обозначить Y(X), то ΔР/P0+1 = Y(X)=(1+а/X)X и возникает сложная функция Y(X), поведение которой при x → ∞ трудно определить. Существует ли предельное значение у величины Y(X) при заданных условиях? Другими словами, чему равен предел функции Y(X) при x → ∞ (если он существует как конечная величина)? Для того, чтобы ответить на возникший вопрос, рассмотрим понятие предела функции в точке. Пусть для определенности выбрана функция Y = 2X и рассматривается процедура приближения величины аргумента x к численному значению X0=3 сначала слева от него, а затем справа. При этом значение функции может также приближаться к какой-либо величине f(x0) = Y0. Пусть X →X0 =3. Тогда, как это следует из таблиц, величина Y → Y0 = 6 как слева, так и справа.
Y 2 4 5 5,6 5,8 …. 6 Y 10 8 7 6,4 6,2 … 6
X 1 2 2,5 2,8 2,9 …. 3 X 5 4 3,5 3,2 3,1 … 3
Если при стремлении аргумента к некоторой точке X0, функция стремится к одному и тому же значению Y0 Как слева так и справа, то говорят, во-первых, что Предел функции в этой точке Существует, а во-вторых, что функция в этой точке Непрерывна.
Теперь можно дать определение предела функции:
Число А называется пределом функции Y = F(X) при X →X0, если для любого сколь угодно малого ε > 0 найдется такое δ > 0, зависящее от ε, что для всех X, для которых справедливо неравенство | X – X0 | < δ верно также неравенство | F(X) – A| < ε.
Используя математическую символику, определение предела можно записать следующим образом:
![]()
В этой записи символ ![]() Заменяет выражение: «для любого», а символ
Заменяет выражение: «для любого», а символ ![]() Переводится как «существует». Двоеточие (:) следует понимать как «такое, что». Двойная стрелка означает равносильность утверждений, стоящих от нее слева и справа.
Переводится как «существует». Двоеточие (:) следует понимать как «такое, что». Двойная стрелка означает равносильность утверждений, стоящих от нее слева и справа.
Для решения конкретных задач поиска пределов различных функций примем без доказательства (которые можно найти в любом подробном курсе математики) перечень основных свойств пределов и необходимых операций.
Свойства пределов и операции с пределами:
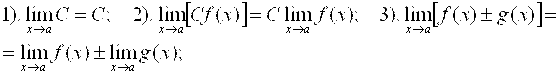 (13)
(13)
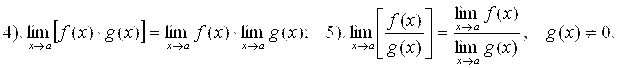
6). ![]() .
.
Пределы, таким образом, описывают Тенденцию, то есть стремление к определенному результату, что безусловно, должно было заинтересовать в первую очередь тех, кто пытается Прогнозировать поведение различных систем. Так, например, известно из истории математики, что при создании теории вероятностей производились многочисленные эксперименты, по исследованию случайных процессов, таких, как бросание игральной кости (кубика), или подбрасывание монеты. При бросании монеты частота появления «герба» (M/N) при многочисленных испытаниях менялась случайным образом, так как это представлено на рис. 13, но при большом количестве опытов (N → ∞), отклонение частоты появления герба от числа, равного 0,5 (50%), становилось все меньше и меньше. Такой эксперимент может повторить каждый человек и найти эту закономерность. Таким образом было доказано, что теоретическое определение вероятности случайного процесса совпадает с частотным значением величины, полученной В пределе при большом количестве испытаний. Если уточнить, что величина M показывает количество «благоприятных исходов», то есть, сколько раз при случайном бросании монеты на поверхность появился герб при общем числе бросаний N, то обнаруженную закономерность можно записать следующим образом:
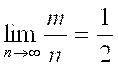
 |

Рис.13. Экспериментальный поиск предела
Экспериментальные закономерности, возникающие при исследовании процессов, выраженные в виде графика неизвестной функции, в общем случае, математически могут быть представлены степенным рядом (7). Достаточно подобрать коэффициенты многочлена при каждом порядковом номере N . Строго доказано, что таким образом можно любую стандартную функцию представить бесконечным степенным рядом (при N→∞). В частности, показательная функция Ex заменяется рядом с коэффициентами, обратно пропорциональными факториалу порядкового номера члена ряда:
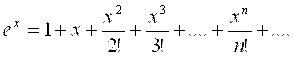 . Факториал числа используется для краткой записи произведения возрастающих чисел. 0! =1, 1!=1, 2!=1∙2, 3!=1∙2∙3, …, n! = 1∙2∙3∙….∙n. С помощью предела замена экспоненциальной функции на степенной ряд запишется следующим образом:
. Факториал числа используется для краткой записи произведения возрастающих чисел. 0! =1, 1!=1, 2!=1∙2, 3!=1∙2∙3, …, n! = 1∙2∙3∙….∙n. С помощью предела замена экспоненциальной функции на степенной ряд запишется следующим образом:
 . (14)
. (14)
Часто при приближенных расчетах используют замену показательной экспоненциальной функции линейной функцией 1+X. Действительно, можно убедится в правильности замены, если проанализировать таблицу значений Ex. Но такое совпадение наблюдается только при малых значениях аргумента, а еще точнее, в интервале 0 < X < 0,1. Этого следовало ожидать, так как для малых значений аргумента квадрат, куб и т. д. степень переменной X дает все меньшую и меньшую величину, которой можно пренебречь при вычислениях.
Таким же образом можно проанализировать стремление к предельному значению отношения двух показательных функций. Очевидно, что при стремлении аргумента к бесконечности, более высокая степень переменной в числителе «побеждает» и результат уходит в бесконечность, а в знаменателе – устремляет дробь к нулю. Если и в числителе, и в знаменателе записана показательная функция с одинаковой степенью, то результат зависит от отношения коэффициентов, стоящих перед аргументом в наивысшей степени, так как остальными членами многочлена с более низкими степенями можно пренебречь. Прямая подстановка значения предела аргумента в отношение двух функций даст неопределенный результат, так как при этом одна бесконечность делится на другую. Говорят, что мы имеем дело с неопределенностью вида [∞/∞]. В общем случае, при поиске предела могут возникать и другие виды неопределенности, например, [0/0].
Аналогичный подход к поиску предела отношения (Sinx)/X показывает, что в таблице значений Sinx в зависимости от X, при малых X, отличие Sinx от X тем меньше, чем ближе величина X подходит к нулю. Следовательно, sinx → x, а отношение этих функций будет стремится к единице при x → 0:
|
. (15)
Формула (15) часто используется при решении задач и в истории математики названа Вторым замечательным пределом. Существует и строгое доказательство справедливости второго замечательного предела. До анализа таблицы, подстановка в числитель и знаменатель предельного значения аргумента x = 0 (так как x→ 0) приводит к неопределенности вида [0/0].
Таким же замечательным признан предел функции (1+1/X)X при X→ ∞, так как он приводит к величине основания натуральных логарифмов Е. Этот предел даже считается определением числа Е.
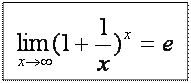
. (16)
Формула (16) названа Первым замечательным пределом.
Применим первый замечательный предел для решения вопроса о предельной выгоде при начислении сложного процента, который был поставлен в начале параграфа. Как определено выше, величина чистой прибыли связана с функцией Y(X) = (1+A/X)X. При переходе к ежедневной, затем к ежечасной, затем к ежеминутной и т. д. процедуре пересчета вклада величина x возрастает. Поэтому найдем предел функции y(x) :
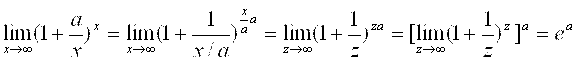 .
.
При вычислении использована замена переменных Z = X/A и свойство (6) пределов, по которому предел от функции в степени A равен степени A предела этой функции. Вычисления показывают, что как бы мелко не дробить процесс перерасчета, чистая прибыль не может превышать величину
 . Расчет суммы накоплений за время T = N – лет при непрерывной процедуре перерасчета, произведенный с помощью первого замечательного предела, приведет к зависимости максимальных накоплений от времени:
. Расчет суммы накоплений за время T = N – лет при непрерывной процедуре перерасчета, произведенный с помощью первого замечательного предела, приведет к зависимости максимальных накоплений от времени:
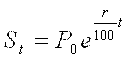 .
.
Видно, что эта функция является экспоненциальной. Чем выше годовой процент, тем более круто поднимется график функции.
В методических рекомендациях (Приложение I) приводятся типичные задачи на вычисление пределов.
| < Предыдущая | Следующая > |
|---|
