02. Линейные функции

Рассматривая пример с функцией, выражающей отношение «деньги-товар», можно представить связь между ними в виде: R=PQ+R0 или записать формулу Y = Kx+ Y0 (1)

Рис. 3. Построение графика линейной функции (а) по таблице и варианты линейных функций (б) в декартовой системе координат

Где R и Q Являются переменными величинами, которые мы переобозначили следующим образом: R = Y и Q = X, а P = K И R0 = Y0 – Постоянны. Величина R0 Может означать доход от реализации товара на предыдущем этапе. Для построения функции вида (1) на графике, по заданным значениям постоянных величин (R0 = 3 и P = 2), выраженных в условных единицах, составляется таблица Y(X) , используя которую строится график так, как это показано на рис. 3а. При построении графика функции по табличным данным подразумевается, что если количество товара Q (жидкость, песок и пр.) теоретически дробимо до сколь угодно малой величины, то множество табличных значений бесконечно. На практике это приводит к непрерывной линии графика функции, все точки которого на рис.3а равноправны и их можно не выделять. Безусловно, в дальнейшем понадобится формализовать свойство непрерывности функций, которое в предыдущем предложении использовано как обычное слово естественного языка. По виду графика функции (1), ее называют Линейной функцией.

Интерпретация графика, изображенного на рис.3а, очевидна: чем больше продано товара, тем больше величина дохода (и наоборот). Ситуация становится менее очевидной, если полученный график функции R(Q) продолжить в сторону отрицательных значений Q (-1,5 ≤ Q ≤ 0 ). На рис. 3б этот вариант изображен под №1 (R1(Q)). Еще один вариант изменений графика получится, если из каждого значения R1 вычесть R0:

R1 – R0 = R2 = PQ + R0 – R0 = PQ → R2 = PQ.

В этом случае график под №2 проходит через начало координат (рис.3б), сохраняя угол наклона β к оси 0Q. Из заштрихованного прямоугольного треугольника (рис.3б), используя определение тригонометрической величины tg β как отношение катета противолежащего углу β к катету прилежащему, получаем при Q = 4 и R2 = 8 следующее соотношение: tg β = 8/4 = 2 = R2/ Q = P. Таким образом, крутизна подъема линейной функции на графике определяется ценой товара, а сдвиг графика функции определяется первоначальными накоплениями R0.

Проведенный анализ показывает, что и в записи линейной функции (1), абстрагируясь от практического смысла использованных величин, параметр k должен характеризовать тангенс угла наклона графика к оси аргумента 0X, а постоянная величина Y0 должна определять смещение графика функции вдоль оси 0Y.

Интерпретацию вариантов, полученных при построении графиков линейной функции на рис.3б, можно назвать проблемой прикладной математики, занимающейся решениями задач, поставленных другими науками или реальной жизнью. Далее, в тех местах учебника, где будет изображен думающий человек (см. рис.3б), следует задуматься (?) и нам над интерпретацией ситуации, представленной графиками функций. Итак (?): Как можно описать ситуацию, соответствующую графикам №2 и №3?

Рассмотрим пример на использование линейной функции в экономике и решим на этой основе некоторые принципиальные вопросы, касающиеся принятия решений, в том числе и административного плана. Речь пойдет о простейшей модели функционирования рынка на базе складывающихся рыночных отношений. Схема рынка и основные обозначения приведены на рис.4. Упрощение модели связано с предположением о том, что рынок стабилен, интересы участников могут быть согласованы, то есть существует рыночное равновесие, производитель товара сам участвует на рынке без посредников, рынок не монополизирован. (?): Каковы функции администрации и управляющего рынком?

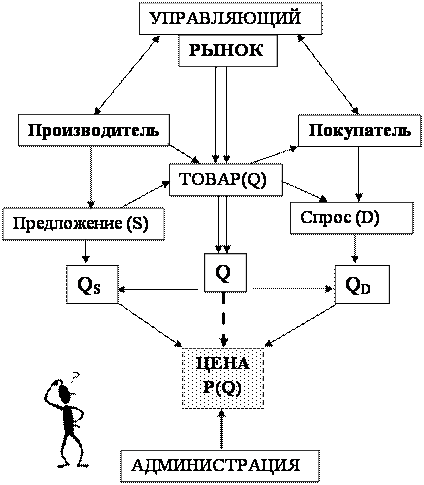
Рис. 4. Упрощенная схематическая модель рынка и рыночных отношений

Выясним, каким образом формируются условия равновесия, при которых интересы производителей и покупателей согласованы. Пусть известно, что спрос на определенные товары может быть неограничен. Тогда по мере поставок товара на рынок, производитель производит и предлагает рынку все большее количество товара по возрастающей цене. Чем больше спрос, тем более высокой может быть цена. Пусть эта зависимость цены от предлагаемого на рынке товара характеризуется линейной функцией. Поэтому можно записать: P(QS) = AQS+P0S. (1)

Другими словами: чем выше цена, по которой на рынке могут купить товар, тем выгоднее производить и поставлять на рынок больше этого товара. Говорят, что соответствующие величины связаны прямой пропорциональной зависимостью. Существует такая минимальная цена (P0S) товара, по которой его не выгодно производить и предлагать (при P = P0S , QS = 0). С другой стороны, спрос ограничен возможностями покупателей и чем ниже цена товара, тем большее его количество раскупается и наоборот, чем выше цена товара, тем меньше его могут купить. В этом случае существует максимальная цена P0D, при которой количество покупаемого товара равно нулю, то есть QD = 0. Пусть в простейшем случае цена уменьшается линейно от максимального значения до минимально возможного. Тогда вид зависимости цены от спроса запишется следующим образом: P(QD ) = P0D – BQD , или при обычной записи линейной функции имеем:

P(QD ) = – BQD + P0D . (2)

Изображая на одном графике обе зависимости спроса и предложения, видим (рис.5), что существует такая точка (М), относительно которой Интересы (спрос и предложение) производителя и покупателя, судя по графикам, начинают резко расходиться и в сторону изменения цены, и в сторону изменения количества товара.

Рис.5. Линии «спроса» и «предложения» в переменных P И Q

Можно административными методами «заморозить» низкие цены (P1), решая при этом социальные задачи защиты малоимущих слоев населения, но возникающая при этом ситуация становится невыгодной для производителя и количество товаров на рынке уменьшается, то есть создается Дефицит. С другой стороны, при лоббировании интересов производителя возможна ситуация на рынке с сохранением административным путем высоких цен на товары (P2). Тогда предложение превышает спрос и создаются «излишки» товара, ведущие к кризису перепроизводства. Таким образом, жесткое администрирование цен не способно решить задачу устойчивой работы рынка.

Возможно, проще понять ситуацию, если считать, что количество товара на рынке зависит от цены и выражать форму этой зависимости в виде функции Q(P). Тогда, функция спроса (2) запишется следующим образом:

QD(P)= - HP + Q0D ,где H = 1/B , а Q0D = P0D/B. Функция предложения (1) будет записана так: QS(P)= KP – Q0S , где K = 1/A, А Q0S = P0S/A.

Рис.6. Динамика рынка

Новые функции также оказались линейными, поэтому попутно доказано следующее утверждение: Если переменная Y линейно зависит от переменной X, то и переменная X линейно зависит от переменной Y.

В результате перехода к новой зависимости количества товара от цены вид графиков измениться так, как это изображено на рис.6. Очевидно, что при цене товара P > PR (в т.1) спрос и предложение резко расходятся. Чтобы товар покупался на рынке, производитель может поступить двумя путями: снизить поставки товара на рынок и создать искусственный дефицит, либо снизить цены на товар (т.2) в ущерб производству. В условиях конкурентного рынка первый путь невозможен, поэтому реально происходит снижение цены, ведущая к общему для всех конкурентов уменьшению производства и созданию дефицита реального. Спрос регулирует этот процесс таким образом, что теперь он превышает предложение и цена товара растет, увеличивая тем самым и производство товаров. Новая цена (т.3) при заданных параметрах спроса и предложения (рис.6) уже ближе к равновесной, но различие между спросом и предложением еще сохраняется. В результате происходит следующий цикл изменения цен и количества товаров, приводящий состояние рынка ближе к равновесию и т. д. до тех пор пока равновесие не наступит. Так выглядит динамика процессов («паутинка») в рамках примитивной модели рынка. Реально, изменение цены товара во времени происходит вдоль линий спроса и предложения.

Для того, чтобы найти параметры равновесного состояния рынка PR и QR ,Необходимо определить в какой точке (М) параметры одинаковы и для спроса и для предложения. Очевидно, что с точки зрения абстрактной математики, необходимо вычислить значения переменных в точке пересечения двух графиков линейных функций: A1X + B1Y = C1

A2x+b2y = c2, (3)

В которых переменные X и Y считаются равноправными, а коэффициенты при них не равны нулю, то есть функция задана в неявном виде. Запишем функции Y(X) в явном виде:

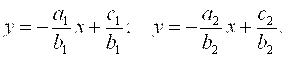В точке пересечения значения функций одинаковы, поэтому приравняем правые части.

. (4)

Подстановка полученного значения аргумента X в функцию Y из верхнего уравнения системы (3) после преобразований приводит к выражению для функции Y в равновесной точке:

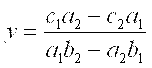. (5)

Таким образом, найдено решение системы (3) из двух уравнений с двумя неизвестными.

Подстановка в полученные решения (4) и (5) соответствующих величин из линейных функций спроса и предложения (рис.5) позволяет вычислить параметры равновесия на рынке.

< Предыдущая		Следующая >