19. Лекция 25. Приближенное вычисление интеграла

Часто нужно вычислить интеграл , а аналитически это сделать невозможно (интеграл не берется) или слишком громоздко. Тогда применяют приближенные методы вычисления интеграла на отрезке, по которым пишут алгоритмы и программы реализации этих методов на ЭВМ. Численный расчет дает значение интеграла с некоторой погрешностью, которая зависит как от погрешности метода, так и от погрешности вычислений. Чаще всего рассматривают равномерную сетку, разбивая отрезок на отрезки длины шагом h: .

1. Формулы прямоугольников.

Обозначим . Заменим интеграл интегральной суммой, вычисляя площадь под графиком функции как сумму площадей прямоугольников с основанием h, высотами .

Если на первом отрезке высоту прямоугольника можно выбрать как , тогда на последнем отрезке высота прямоугольника . Получим Первую формулу прямоугольников

.

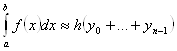Если на первом отрезке высоту прямоугольника можно выбрать как , тогда на последнем отрезке высота прямоугольника . Получим Вторую формулу прямоугольников

.

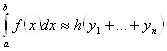Оценим погрешность формул прямоугольников. Разложим в ряд Тейлора и оценим остаточный член.

Для первой формулы прямоугольников

Где .

Для второй формулы прямоугольников

Где .

Таким образом, обе формулы прямоугольников дают погрешность порядка h и являются формулами первого порядка точности.

Можно повысить точность формулы прямоугольников За счет вычисления функции в серединах отрезков разбиения. Получаем Третью формулу прямоугольников

.

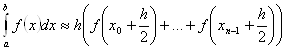Оценим погрешность этой формулы.

+

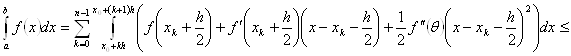
+0+

Таким образом, погрешность третьей формулы прямоугольников не превышает , где . Эта формула прямоугольников имеет второй порядок точности.

2. Формула трапеций.

Сложим первую и вторую формулы прямоугольников и разделим пополам. Получим Формулу трапеций

Поясним название формулы. Приблизим площадь под графиком функции на отрезке площадью трапеции . Суммируя площади по всему отрезку интегрирования, получим

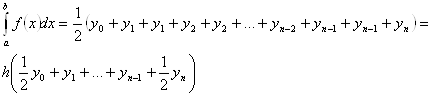
Аппроксимируем функцию кусочно – линейной функцией, значения которой совпадают с значениями функции в точках разбиения. Площадь под графиком кусочно – линейной функции на отрезке составит

. Суммируя площади по всему отрезку интегрирования, получим вновь формулу трапеций.

Можно показать, что формула трапеций – формула второго порядка точности. Погрешность вычисления интеграла с помощью этой формулы (это можно показать) не превышает , т. е. в два раза больше, чем по третьей формуле прямоугольников.

3. Формула Симпсона.

Аппроксимируем функцию На отрезке разбиения квадратичной функцией так, чтобы

Лемма. .

Докажем лемму для . Сделаем замену .

Тогда формула сведется к следующей:

.

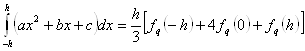Левая часть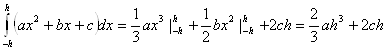

Правая часть . Лемма доказана.

Разобьем теперь отрезок интегрирования на 2n частей, (). Применим лемму к отрезкам , ,..., получим Формулу Симпсона

.

Можно показать, что формула Симпсона – Формула четвертого порядка точности, ее погрешность не превосходит , где . Это означает, что при интегрировании многочлена третьей степени формула Симпсона точна, ее погрешность равна нулю.

Пример. Вычислить приближенно I =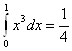 с шагом .

1 формула прямоугольников ,

2 формула прямоугольников ,

3 формула прямоугольников ,

Формула трапеций .

Формула Симпсона

< Предыдущая		Следующая >