18. Лекции 23-24. Устойчивость движения, классификация точек покоя, теоремы Ляпунова

Рассмотрим нелинейную систему дифференциальных уравнений, запишем ее уравнения в векторной форме

Или в координатной форме

В качестве независимой переменной выбрано время t, поэтому система дифференциальных уравнений является моделью некоторого процесса – изменения переменной во времени или Движения материальной точки, Занимающей в фазовом пространстве текущее положение и изменяющей это положение с изменением времени t. Таким образом, Движение – это частное решение системы дифференциальных уравнений.

Зададим некоторые начальные условия . Пусть выполняются условия теоремы Коши (непрерывны в рассматриваемой области). Тогда через любую точку расширенного фазового пространства из рассматриваемой области проходит единственная интегральная кривая – график частного решения . Назовем движение, «начинающееся» в точке Невозмущенным движением . Если «возмутить» – несколько изменить начальные условия в фазовом пространстве, выбрать их , то изменится и движение. Назовем движение, «начинающееся» в точке , Возмущенным движением . Если возмущение начальных условий невелико, то в некоторой окрестности начальной точки траектории – движения тоже близки.

Справедлива Теорема о непрерывности решения по начальным условиям. Пусть выполнены условия теоремы Коши. Тогда

Отсюда видно, что близость возмущенного и невозмущенного движений гарантируется В некоторой временной окрестности, размер которой зависит от размеров трубки – окрестности («допуска») в фазовом пространстве координат.

Однако в практике встречаются процессы, для которых надо гарантировать близость возмущенного и невозмущенного движений «вообще», при любом времени t > T (важно, чтобы существовало это некоторое T).

Например, запустив спутник на орбиту, полезно быть уверенным, что он не свалится нам на голову через 10 или 100 лет, а будет «вечно» находиться на орбите.

В наше время приходится сталкиваться с экологическими проблемами. Кто же знал, конструируя двигатель внутреннего сгорания, что через некоторое время использование этого открытия поставит под угрозу существование жизни на Земле?

Рассматривая близость возмущенного и невозмущенного движений «вообще», при любом времени t > T, мы приходим к определению Устойчивости движения по Ляпунову.

Движение называется Устойчивым по Ляпунову, Если

Смысл определения в том, что для любого размера окрестности «допуска» (по фазовым координатам) невозмущенного движения существует размер окрестности, в которой можно «возмутить» начальные условия. Причем это возмущение приведет к тому, что возмущенное движение после некоторого момента времени Т войдет в окрестность «допуска» и останется в этой окрестности при любом t > T.

Если движение устойчиво по Ляпунову и , то такое движение называется Асимптотически устойчивым.

Если движение асимптотически устойчиво, то возмущенное движение с ростом времени стремится к невозмущенному.

Движение называется Неустойчивым по Ляпунову, если

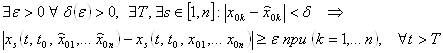
Смысл этого определения в том, что как бы ни было мало возмущение начальных условий, все равно со временем хотя бы по одной координате возмущенное движение выйдет из некоторой окрестности «допуска» невозмущенного движения.

Теорема. Задача об устойчивости движения может быть сведена к задаче об устойчивости тривиального (тождественно равного нулю) решения системы.

Доказательство. Обозначим . Тогда

При Имеем , поэтому задача об устойчивости движения для исходной системы уравнений может быть заменена эквивалентной ей задачей об устойчивости тривиального решения для системы

Поэтому обычно заранее делают указанную замену и исследуют задачу об устойчивости тривиального решения.

Таким образом, задача об устойчивости движения может быть сведена для автономной системы к исследованию характера ее точки покоя (при рассмотрении свойств автономных систем было показано: если - точка покоя, то - решение системы).

Устойчивость по первому приближению.

Будем рассматривать автономную систему

И ее «систему первого приближения»

Заметим, что систему первого приближения можно строить, линеаризуя в окрестности нуля элементы матрицы, заменяя бесконечно малые элементы матрицы эквивалентными.

Теорема Ляпунова об устойчивости по первому приближению.

Пусть 1) непрерывны и непрерывно дифференцируемы по ,

2) .

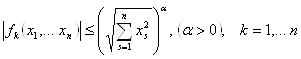Если все собственные числа матрицы A системы первого приближения имеют отрицательные действительные части, то тривиальное решение устойчиво.

Если хотя бы одно собственное число имеет положительную действительную часть, то тривиальное решение неустойчиво.

Пример.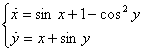

Система первого приближения

Тривиальное решение неустойчиво.

Пример.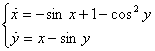

Система первого приближения

Тривиальное решение устойчиво.

Поскольку для автономных систем анализ устойчивости тривиального решения сводится к исследованию характера точки покоя, то зная поведение решений в окрестности различных точек покоя, мы выясним тем самым поведение траекторий систем.

Классификация точек покоя для автономных систем второго и третьего порядков.

Система второго порядка.

Запишем уравнение автономной системы второго порядка

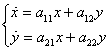. Точка покоя .

1. Корни характеристического уравнения действительны..

А) .

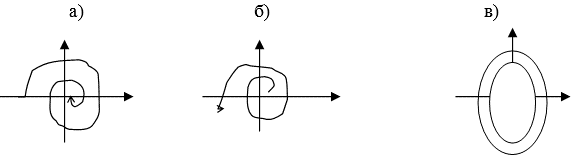
При . Поэтому точка покоя (или тривиальное решение) асимптотически устойчива.

Заметим, что первое слагаемое – это проекция траектории на ось , второе слагаемое – проекция на ось .

Такая точка покоя называется Устойчивый узел.

Б) .

Этот случай можно рассматривать как предыдущий, если формально положить t < 0. Получим те же траектории, что и в п. а), но стрелки на них будут направлены в другую сторону. Направление движение другое (t<0). Такая точка называется Неустойчивый узел.

В) .

По вектору мы, находясь на траектории, стремимся к нулю, по вектору , наоборот, удаляемся от нуля.

Такая точка покоя - Седло.

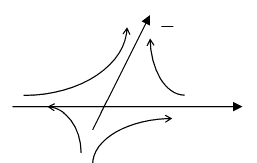
Г) .

Это – тоже седло, но стрелки

Направлены в другую сторону.

Траектория прижимается к той оси, для которой модуль характеристического числа меньше.

Седла – неустойчивые точки покоя.

Заметим, в ситуациях узлов и седла траектория, начавшись в определенном квадранте, в нем и остается.

Д) .

Точка покоя – Дикритический узел,

Устойчивый при , неустойчивый при

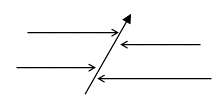
Е)

Точка покоя - Вырожденный узел, При устойчивая, но не асимптотически устойчивая. Если , то точка покоя - неустойчивая (стрелки направлены в обратную сторону)

Ж) . Точка безразличного равновесия. При изменении времени любая точка остается на месте. Этими точками заполнена вся плоскость.

2. Корни характеристического уравнения комплексно сопряженные.

Параметр t имеет смысл угла поворота вокруг начала координат (в периодической составляющей).

А) Если, то траектория приближается к началу координат с ростом t (спираль), так как - убывающая функция. Точка покоя Устойчивый фокус Асимптотически устойчива

Б) если , то траектория удаляется от начала координат с ростом t (спираль), так как - возрастающая функция. Точка покоя Неустойчивый фокус неустойчива

В) если , то траектории представляют собой эллипсы, охватывающие начало координат. Точка покоя Центр Устойчива, но не асимптотически устойчива.

Пример. , ,

Классифицировать точки покоя в зависимости от параметра.

А) седло,

Б) неустойчивый узел

В) вырожденный узел

2) - комплексно сопряженные.

Так как , то точка покоя – неустойчивый фокус

3) , точка покоя – неустойчивый дикритический узел.

Система третьего порядка.

Запишем уравнение автономной системы третьего порядка

1) Все корни характеристического уравнения действительны и различны.

Картину поведения фазовых траекторий довольно легко представить, рассматривая поведение фазовых траекторий в плоскостях, натянутых на пары собственных векторов. Этот случай уже изучен выше.

А)

В плоскостях , , , имеем устойчивые узлы. Такая точка покоя так и называется – Устойчивый узел.

Б) В плоскостях , , , имеем неустойчивые узлы. Такая точка покоя называется – Неустойчивый узел.

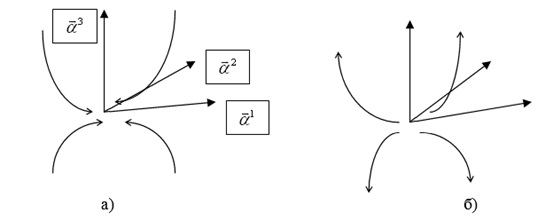
В) один корень имеет знак, противоположный остальным двум корням. Точка покоя в этом случае называется Седло – узел И является неустойчивой точкой покоя.

Пусть, например, . Тогда в плоскости имеем неустойчивый узел, а в плоскостях , - седла. Если , то в плоскости имеем устойчивый узел, а в плоскостях , - седла.

Заметим, что в ситуациях узлов и седла – узел траектория, начавшись в определенном октанте, не переходит в другой октант.

2) - действительный корень характеристического уравнения, - комплексно сопряженная пара корней.

Заметим, что при изменении номера корней ситуация будет аналогичной.

В плоскости имеем фокус, устойчивый при , неустойчивый при .

А) . Такая точка покоя называется Устойчивый фокус.

Б) . Такая точка покоя называется Неустойчивый фокус.

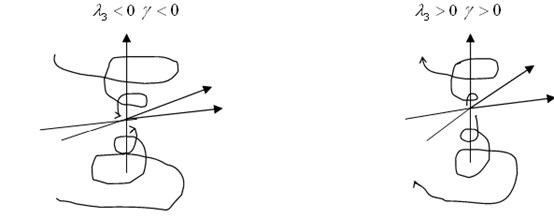
В) или . Такая особая точка называется Седло – фокус и является неустойчивой.

В первом случае по оси Точка по траектории приближается к плоскости и уходит от начала координат, так как на самой плоскости имеем неустойчивый фокус.

Во втором случае на плоскости имеем устойчивый фокус, поэтому траектория стремится к оси , но удаляется от начала координат по этой оси, так как .

Функция Ляпунова, «вторая метода Ляпунова».

Рассмотрим автономную систему 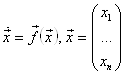И

Функцию .

Назовем эту функцию Знакоположительной, если ,

Знакоотрицательной, если

Назовем функцию Положительно определенной, Если

1) она знакоположительна,

Назовем функцию Отрицательно определенной, Если

1) она знакоотрицательна,

Назовем функцию Знакоопределенной, Если она является отрицательно определенной или положительно определенной.

Введем Производную функции в силу системы : . Заметим, что . Поэтому, если , то угол между градиентом V и вектором правых частей системы тупой. Следовательно, убывание функции V соответствует движению по фазовым траекториям внутрь линии уровня =С.

На этом основан Метод функций Ляпунова. Этот метод сводится к трем теоремам Ляпунова.

Теорема Ляпунова об устойчивости. Пусть существует функция (функция Ляпунова), положительно определенная и имеющая знакоотрицательную в некоторой окрестности точки .

Тогда тривиальное решение автономной системы устойчиво по Ляпунову.

Теорема Ляпунова об асимптотической устойчивости. Пусть существует функция , положительно определенная и имеющая отрицательно определенную в некоторой окрестности точки .

Тогда тривиальное решение автономной системы асимптотически устойчиво по Ляпунову.

Теорема Ляпунова о неустойчивости. Пусть . Пусть знакоопределена в некоторой окрестности точки . Если в любой окрестности точки найдутся такие точки, в которых знаки и совпадают, то тривиальное решение автономной системы неустойчиво.

Пример.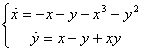

Выберем

Положительно определена, Отрицательно определена. Поэтому тривиальное решение асимптотически устойчиво.

Пример.

Выберем

И положительно определены, поэтому тривиальное решение неустойчиво.

< Предыдущая		Следующая >