20. Лекция 26. Обзор численных методов решения задачи Коши для обыкновенных дифференциальных уравнений

Будем рассматривать схемы численных методов для уравнения первого порядка

Это – самый простой случай, но к нему по аналогии сводятся схемы методов для системы дифференциальных уравнений и для дифференциального уравнения n - го порядка.

1. Методы, основанные на разложении функции в ряд Тейлора.

Запишем разложение функции в ряд Тейлора в окрестности точки

Рассмотрим равномерную сетку по

Пусть , тогда разложение функции в ряд Тейлора можно записать в виде

, где

Подставим в из дифференциального уравнения

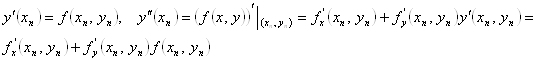Тогда

Это – основная расчетная формула.

Учитывая в слагаемые с производными высших порядков, получим более точные приближенные формулы.

Если взять , то получим Метод Эйлера

2. Методы Рунге – Кутта.

Основная идея методов Рунге – Кутта – вместо вычисления производных высших порядков в вычислять значения функции в некоторых точках, отличных от .

Выберем

Разложим по h

= +=

Сравним с приведенной выше основной расчетной формулой

И определим коэффициенты

Пусть , тогда .

Если . Тогда

= .

Это – Метод Хойна.

Если в формуле . Выбрать ,

То получим Явный M – шаговый (M – точечный) метод Рунге – Кутта.

Наиболее распространен явный четырехточечный метод Рунге – Кутта

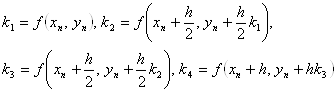
В явных методах Рунге – Кутта значения вычисляются только по предыдущим значениям .

В Неявных методах Рунге – Кутта значения вычисляются как по предыдущим, так и по последующим значениям . Поэтому в этих методах приходится еще решать систему уравнений относительно .

Неявный M – шаговый метод Рунге – Кутта Можно записать в виде

3. Методы Адамса.

Идея методов Адамса – использовать не промежуточные вычисления значений правой части дифференциального уравнения внутри отрезка , а значения правой части на предыдущих шагах (сделать метод методом «с памятью»).

В формуле 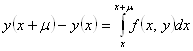заменим интерполяционным полиномом Ньютона .

Явные методы Адамса (Адамса – Башфорта).

Возьмем , но интеграл будем брать по предыдущему отрезку . Тогда

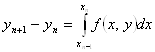
Здесь - конечная разность - го порядка:

Подставляя эти разности, получим

(K – шаговый явный метод Адамса – Башфорта)

Пример. Получен Явный метод Адамса – Башфорта второго порядка (Двухшаговый)

Более точен метод Адамса – Башфорта четвертого порядка:

Заметим, если задано (в задаче Коши начальное условие задается), то для того, чтобы начал работать метод Адамса 4 порядка, нужно вычислить еще значения (каким-либо другим методом) . Тогда из системы формул Адамса Башфорта, выписанных для , вычисляются значения правых частей , необходимые для того, чтобы метод начал работать. Затем уже по этим значениям по формуле метода определяются .

Эта процедура называется «разгоном метода» и является обязательной в методах Адамса.

Неявные методы Адамса (Адамса – Мултона).

Возьмем , интеграл будем брать по отрезку . Тогда

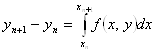
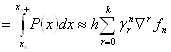
Здесь - конечная разность - го порядка:

Подставляя эти разности, получим

(K – шаговый явный метод Адамса –Мултона)

Формально он записан в том же виде, что и метод Адамса – Башфорта, но разница существенна: в методе Адамса – Мултона в левой части уравнения присутствует , а в правой части присутствует . Поэтому приходится еще решать систему уравнений для явного определения .

Пример. . Поэтому имеем формулу

Метода Адамса – Мултона второго порядка.

Более точен Метод Адамса – Мултона четвертого порядка

Эти методы также требуют разгона.

Обобщением методов Адамса являются Линейные многошаговые методы

Если , то метод – явный, если , то метод – неявный.

Есть методы, сочетающие явные и неявные этапы – методы. Таковы, например, методы типа Предиктор – корректор (предиктор P – предсказатель – явный метод, корректор С – неявный метод). Эти методы содержат обычно и этапы вычисления функции Е. Распространены методы РЕСЕ и РЕС.

Рассмотрим в качестве метода Р метод Адамса – Башфорта 2 го порядка, а в качестве метода С – метод Адамса – Мултона 2 го порядка.

Схема метода может быть записана в виде.

Р .

Метод Р «предсказывает», прогнозирует , вычисляется значение правой части, которое используется в методе С – «корректоре» для коррекции приближения , затем вычисляется более точное значение правой части, которое вновь используется в методе Р.

Сходимость, устойчивость разностных схем, порядок точности методов.

Вообще-то это – тема отдельного курса, но нельзя говорить о методах решения дифференциальных уравнений и не сказать хотя бы несколько слов о сходимости численных алгоритмов, устойчивости вычислительных схем и точности методов.

Рассмотрим дифференциальное уравнение , равномерную сетку на отрезке интегрирования .

Рассмотрим сеточную функцию - правую часть уравнения, определенную на сетке .

Введем аппроксимации производной:

, , .

Задача Коши (дифференциальная задача) заменяется Разностной задачей (Разностной схемой)

Или .

Разностная схема отличается от дифференциального уравнения тем, что функции заменены сеточными, производные заменены их аппроксимациями.

- решение разностной задачи, - решение дифференциальной задачи, - сеточная функция, построенная по .

Сходимость разностной схемы с порядком .

Решение сходится к с порядком , если .

Аппроксимация с порядком .

Пусть задача имеет единственное решение.

Пусть (- невязка).

Разностная задача аппроксимирует дифференциальную задачу на решении

с порядком , если .

Пример. Рассмотрим схему Эйлера для задачи .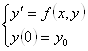

Разностная задача , ,

. Поэтому

=. То есть, , следовательно, схема Эйлера дает аппроксимацию первого порядка.

Замечание. Ошибку аппроксимации Можно оценить по Правилу Рунге, решая дифференциальное уравнение с шагом , а затем с шагом И сравнивая решения: , где - порядок аппроксимации.

Устойчивость разностной схемы.

Разностная схема называется Устойчивой, Если Разностная задача имеет единственное решение такое, что .

Другими словами, при малых возмущениях Мало возмущается .

Теорема. Пусть разностная схема аппроксимирует дифференциальную задачу на решении с порядком и устойчива. Тогда решение разностной задачи сходится к с порядком , причем . Здесь - константа аппроксимации, С – константа устойчивости.

Доказательство. Пусть , тогда по единственности решения (определение устойчивости) и определению аппроксимации . Тогда

(при имеем ).

< Предыдущая