07. Лекции 7-8 Несобственные интегралы
Мы строили определенный интеграл По отрезку ![]() - конечные числа, т. е. по конечному промежутку числовой оси.
- конечные числа, т. е. по конечному промежутку числовой оси.
Кроме того, предполагалось, что подынтегральная Функция непрерывна на отрезке или имеет на нем конечное число точек разрыва первого рода.
Если снимается хотя бы одно из этих условий, то понятие интеграла надо обобщать, вводя в прежней конструкции интеграла предельный переход и получая так называемые Несобственные интегралы. Если снимается первое условие, то мы имеем несобственный интеграл первого рода, если снимается второе условие, то мы имеем несобственный интеграл второго рода.
Несобственные интегралы от непрерывной функции по бесконечному промежутку (первого рода).
Пусть отрезок ![]() числовой оси неограничен. Это возможно в трех случаях:
числовой оси неограничен. Это возможно в трех случаях: ![]() . Определим несобственные интегралы как пределы
. Определим несобственные интегралы как пределы
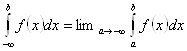 ,
,
 ,
,
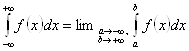 . В последнем интеграле a и b независимо друг от друга стремятся к
. В последнем интеграле a и b независимо друг от друга стремятся к ![]() . Если
. Если ![]() , то предел в правой части последнего равенства называется главным значением несобственного интеграла.
, то предел в правой части последнего равенства называется главным значением несобственного интеграла.
Если эти пределы существуют и конечны, то несобственные интегралы называются Сходящимися. Если предел не существует или бесконечен, то такой несобственный интеграл называется Расходящимся.
Если сходятся интегралы от функций ![]() , то сходятся интегралы от функций
, то сходятся интегралы от функций ![]() . Это следует из теорем о пределах.
. Это следует из теорем о пределах.
Пример. ![]() , интеграл сходится.
, интеграл сходится.
Пример. ![]() , интеграл расходится.
, интеграл расходится.
Пример. ![]() сходится при
сходится при ![]() и расходится при
и расходится при ![]() . Проверьте это.
. Проверьте это.
Рассмотрим Интеграл Дирихле ![]() .
.
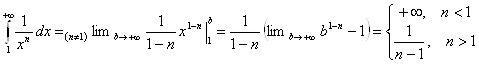 .
.
При ![]()
![]() , интеграл расходится.
, интеграл расходится.
Итак, Несобственный интеграл Дирихле первого рода ![]() сходится при
сходится при ![]() расходится при
расходится при ![]()
Признаки сравнения несобственных интегралов (достаточные признаки сходимости и расходимости несобственных интегралов).
1 признак. Теорема. Пусть при ![]() выполнено неравенство
выполнено неравенство ![]() .
.
Если интеграл 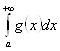 сходится, то и интеграл
сходится, то и интеграл 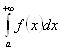 сходится.
сходится.
Если интеграл 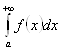 расходится, то и интеграл
расходится, то и интеграл 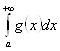 расходится.
расходится.
Доказательство. Проинтегрируем неравенство ![]() на отрезке
на отрезке ![]() ,
,
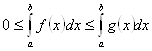 . Так как обе функции на отрезке имеют только положительные значения, то интегралы от этих функций представляют собой возрастающие функции от верхнего предела b.
. Так как обе функции на отрезке имеют только положительные значения, то интегралы от этих функций представляют собой возрастающие функции от верхнего предела b.
Если 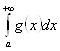 сходится (
сходится (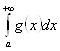 = I), то при любом b > a
= I), то при любом b > a ![]()
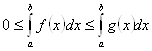
![]()
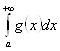 = I (I – конечное число).
= I (I – конечное число).
Поэтому  - монотонно возрастающая, ограниченная функция верхнего предела интегрирования b. Следовательно, по теореме Вейерштрасса этот интеграл как функция b имеет предел
- монотонно возрастающая, ограниченная функция верхнего предела интегрирования b. Следовательно, по теореме Вейерштрасса этот интеграл как функция b имеет предел
 , т. е. интеграл
, т. е. интеграл 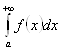 Сходится.
Сходится.
Пусть теперь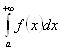 расходится. Если
расходится. Если 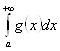 сходится, то по доказанному и
сходится, то по доказанному и 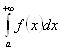 сходится, противоречие. Теорема доказана.
сходится, противоречие. Теорема доказана.
Вообще-то, все было ясно из геометрического смысла определенного интеграла как площади криволинейной трапеции под графиком функции. Если значения одной функции больше, чем значения другой функции, то и соответствующая криволинейная трапеция имеет большую площадь. И если эта площадь конечна, то и меньшая площадь конечна. А если меньшая площадь бесконечна, то и большая площадь бесконечна. Но строгое доказательство не подведет, а «очевидное» иногда подводит.
2 признак сравнения. Теорема. Пусть при x>a ![]() . Если существует конечный предел
. Если существует конечный предел ![]() , то интегралы
, то интегралы 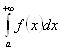 ,
,  , сходятся или расходятся одновременно (если один сходится, то и другой сходится, если один расходится, то и другой расходится).
, сходятся или расходятся одновременно (если один сходится, то и другой сходится, если один расходится, то и другой расходится).
Доказательство. Из определения предела следует ![]()
![]() .
.
Если интеграл 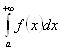 сходится, то по первому признаку сравнения сходится интеграл
сходится, то по первому признаку сравнения сходится интеграл  , а, следовательно, сходится интеграл
, а, следовательно, сходится интеграл 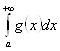 . Если интеграл
. Если интеграл 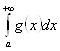 сходится, то сходится интеграл
сходится, то сходится интеграл 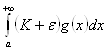 , а, следовательно, по первому признаку сравнения сходится интеграл
, а, следовательно, по первому признаку сравнения сходится интеграл 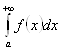 . Пусть интеграл
. Пусть интеграл 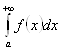 расходится. Если интеграл
расходится. Если интеграл 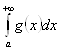 сходится, то по первому признаку сравнения сходится интеграл
сходится, то по первому признаку сравнения сходится интеграл 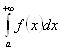 , противоречие. Пусть интеграл
, противоречие. Пусть интеграл 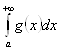 расходится. Если интеграл
расходится. Если интеграл 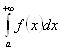 сходится, то по первому признаку сравнения сходится интеграл
сходится, то по первому признаку сравнения сходится интеграл 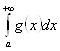 , противоречие. Теорема доказана.
, противоречие. Теорема доказана.
Эталонами служат обычно интегралы Дирихле или интегралы от показательной функции.
Пример. ![]() сходится по второму признаку сравнения, интеграл сравнения
сходится по второму признаку сравнения, интеграл сравнения ![]() .
.
Пример. ![]() сходится по первому признаку, интеграл сравнения
сходится по первому признаку, интеграл сравнения
![]() .
.
Несобственные интегралы от разрывной функции по конечному промежутку (второго рода).
Функция может терпеть разрыв на левом конце отрезка ![]() , на правом конце или в некоторой внутренней точке с отрезка.
, на правом конце или в некоторой внутренней точке с отрезка.
Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() за исключением точки x= a, тогда несобственным интегралом второго рода от функции
за исключением точки x= a, тогда несобственным интегралом второго рода от функции ![]() по отрезку
по отрезку ![]()
 Называется предел
Называется предел 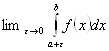 =
=
.
Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() за исключением точки x= b, тогда несобственным интегралом второго рода от функции
за исключением точки x= b, тогда несобственным интегралом второго рода от функции ![]() по отрезку
по отрезку ![]()
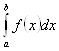 называется предел
называется предел 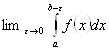 =
=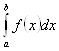 .
.
Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() за исключением точки x=
за исключением точки x= ![]() , тогда несобственным интегралом второго рода от функции
, тогда несобственным интегралом второго рода от функции ![]() по отрезку
по отрезку ![]() называется
называется  =
=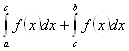 (интегралы в правой части определены выше).
(интегралы в правой части определены выше).
Если указанные пределы существуют и конечны, то интегралы называются Сходящимися, если предел бесконечен или не существует вообще, то интеграл Расходится.
Если сходятся интегралы от функций ![]() , то сходятся интегралы от функций
, то сходятся интегралы от функций ![]() . Это следует из теорем о пределах.
. Это следует из теорем о пределах.
Пример. 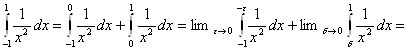
![]() Интеграл расходится, так как пределы в правой части равенства бесконечны.
Интеграл расходится, так как пределы в правой части равенства бесконечны.
Заметим, если здесь формально применить формулу Ньютона-Лейбница (она неприменима, т. к. функция разрывна), получим ответ 2. Еще раз убеждаемся, что теоремы следует применять, внимательно проверяя условия их применимости.
Рассмотрим Несобственный интеграл Дирихле второго рода 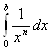 .
.
 .
.
При ![]()
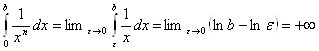 , интеграл расходится.
, интеграл расходится.
Итак, Несобственный интеграл Дирихле второго рода 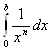 сходится при
сходится при ![]() расходится при
расходится при ![]()
Замечание. Интегралы Дирихле первого и второго рода расходятся при n=1. При n>1 интеграл Дирихле первого рода сходится, а интеграл Дирихле второго рода расходится. При n<1 интеграл Дирихле первого рода расходится, а интеграл Дирихле второго рода сходится.
Признаки сравнения интегралов остаются верными и для интегралов второго рода. Эталонами сравнения служат обычно интегралы Дирихле и интегралы от показательной функции.
Примеры.  сходится сравнением с несобственным интегралом Дирихле
сходится сравнением с несобственным интегралом Дирихле ![]() (n=
(n=![]() ) по второму признаку сравнения. Вспомните, что сумма бесконечно малых функций в знаменателе эквивалентна при
) по второму признаку сравнения. Вспомните, что сумма бесконечно малых функций в знаменателе эквивалентна при ![]() бесконечно малой наинизшего порядка малости. Можно доказать эквивалентность непосредственным вычислением предела.
бесконечно малой наинизшего порядка малости. Можно доказать эквивалентность непосредственным вычислением предела.
![]() расходится сравнением с интегралом
расходится сравнением с интегралом ![]() по второму признаку сравнения.
по второму признаку сравнения.
Абсолютная сходимость несобственных интегралов.
До сих пор при анализе сходимости несобственных интегралов мы предполагали, что подынтегральная функция принимает только положительные значения. Откажемся от этого предположения. Будем исследовать сходимость несобственных интегралов Первого рода вида 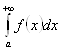 , где
, где ![]() может принимать значения любого знака. Полученные результаты переносятся по аналогии на остальные несобственные интегралы первого и второго рода.
может принимать значения любого знака. Полученные результаты переносятся по аналогии на остальные несобственные интегралы первого и второго рода.
Интеграл 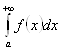 Называется Абсолютно сходящимся, если сходится несобственный интеграл
Называется Абсолютно сходящимся, если сходится несобственный интеграл 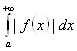 .
.
Теорема. Если интеграл  абсолютно сходится, то он сходится.
абсолютно сходится, то он сходится.
Доказательство. Введем в рассмотрение две вспомогательные функции ![]() . Эти функции принимают только положительные значения. Кроме того,
. Эти функции принимают только положительные значения. Кроме того, ![]() . По первому признаку сравнения из абсолютной сходимости интеграла
. По первому признаку сравнения из абсолютной сходимости интеграла , т. е. из сходимости интеграла
, т. е. из сходимости интеграла 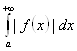 следует сходимость интегралов
следует сходимость интегралов  ,
, 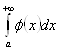 . Тогда сходится интеграл
. Тогда сходится интеграл  . Теорема доказана.
. Теорема доказана.
Пример. 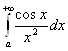 Абсолютно сходится, так как
Абсолютно сходится, так как ![]() А интеграл
А интеграл  сходится.
сходится.
Условная сходимость несобственных интегралов.
Интеграл  называется Условно сходящимся, если он сходится, а интеграл
называется Условно сходящимся, если он сходится, а интеграл 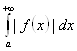 расходится.
расходится.
Покажем, что интеграл  Условно сходится.
Условно сходится.

Перейдем к пределу при ![]() . Интеграл в правой части равенства абсолютно сходится, обозначим его I.
. Интеграл в правой части равенства абсолютно сходится, обозначим его I.
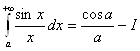 . Поэтому интеграл
. Поэтому интеграл  Сходится.
Сходится.
Покажем, что этот интеграл не сходится абсолютно. Справедливо неравенство ![]() .
. 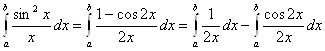 .
.
Переходя к пределу при ![]() , видим, что интеграл
, видим, что интеграл 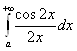 Сходится (аналогично интегралу
Сходится (аналогично интегралу 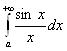 ), интеграл
), интеграл 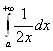 расходится. Поэтому интеграл
расходится. Поэтому интеграл 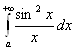 расходится. Если бы он сходился, то складывая его с сходящимся интегралом 0.5
расходится. Если бы он сходился, то складывая его с сходящимся интегралом 0.5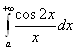 , получили бы сходящийся интеграл (0.5
, получили бы сходящийся интеграл (0.5![]() ), а этот интеграл расходится.
), а этот интеграл расходится.
Используя неравенство ![]() и расходимость интеграла
и расходимость интеграла 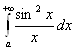 , по первому признаку сравнения получаем расходимость интеграла
, по первому признаку сравнения получаем расходимость интеграла 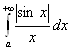 . Следовательно, интеграл
. Следовательно, интеграл 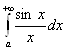 Условно сходится.
Условно сходится.
| < Предыдущая | Следующая > |
|---|