08. Лекции 9-10. Приложения определенного интеграла

Приложение интеграла к физическим задачам основано на свойстве аддитивности интеграла по множеству. Поэтому с помощью интеграла могут вычисляться такие величины, которые сами аддитивны по множеству. Например, площадь фигуры равна сумме площадей ее частей Длина дуги, площадь поверхности, объем тела, масса тела обладают тем же свойством. Поэтому все эти величины можно вычислять с помощью определенного интеграла.

Можно использовать два метода решения задач: Метод интегральных сумм и метод дифференциалов.

Метод интегральных сумм повторяет конструкцию определенного интеграла: строится разбиение, отмечаются точки, в них вычисляется функция, вычисляется интегральная сумма, производится предельный переход. В этом методе основная трудность – доказать, что в пределе получится именно то, что нужно в задаче.

Метод дифференциалов использует неопределенный интеграл и формулу Ньютона – Лейбница. Вычисляют дифференциал величины, которую надо определить, а затем, интегрируя этот дифференциал, по формуле Ньютона – Лейбница получают требуемую величину. В этом методе основная трудность – доказать, что вычислен именно дифференциал нужной величины, а не что-либо иное.

Вычисление площадей плоских фигур.

1. Фигура ограничена графиком функции, заданной в декартовой системе координат.

Мы пришли к понятию определенного интеграла от задачи о площади криволинейной трапеции (фактически, используя метод интегральных сумм). Если функция принимает только неотрицательные значения, то площадь Под графиком функции на отрезке [a, b] может быть вычислена с помощью определенного интеграла 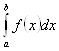. Заметим, что Поэтому здесь можно увидеть и метод дифференциалов.

Но функция может на некотором отрезке принимать и отрицательные значения, тогда интеграл по этому отрезку будет давать отрицательную площадь, что противоречит определению площади.

Можно вычислять площадь по формуле S=. Это равносильно изменению знака функции в тех областях, в которых она принимает отрицательные значения.

Если надо вычислить площадь фигуры, ограниченной сверху графиком функции , а снизу графиком функции , то Можно пользоваться формулой S=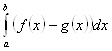, так как .

Пример. Вычислить площадь фигуры, ограниченной прямыми x=0, x=2 и графиками функций y=x2, y=x3.

Заметим, что на интервале (0,1) выполнено неравенство x2 > x3, а при x >1 выполнено неравенство x3 > x2. Поэтому

2. Фигура ограничена графиком функции, заданной в полярной системе координат.

Пусть график функции задан в полярной системе координат и мы хотим вычислить площадь криволинейного сектора, ограниченного двумя лучами и графиком функции в полярной системе координат.

Здесь можно использовать метод интегральных сумм, вычисляя площадь криволинейного сектора как предел суммы площадей элементарных секторов, в которых график функции заменен дугой окружности .

Можно использовать и метод дифференциалов: .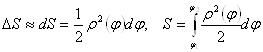

Рассуждать можно так. Заменяя элементарный криволинейный сектор, соответствующий центральному углу круговым сектором, имеем пропорцию . Отсюда . Интегрируя и используя формулу Ньютона – Лейбница, получаем .

Пример. Вычислим площадь круга (проверим формулу). Полагаем . Площадь круга равна .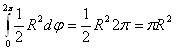

Пример. Вычислим площадь, ограниченную кардиоидой .

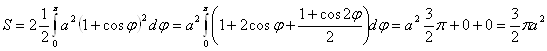
3 Фигура ограничена графиком функции, заданной параметрически.

Функция может быть задана параметрически в виде . Используем формулу S=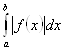, подставляя в нее и пределы интегрирования по новой переменной . . Обычно при вычислении интеграла выделяют те области, где подынтегральная функция имеет определенный знак и учитывают соответствующую площадь с тем или иным знаком.

Пример. Вычислить площадь, ограниченную эллипсом .

Используем симметрию эллипса, вычислим площадь четверти эллипса, находящуюся в первом квадранте. В этом квадранте . Поэтому .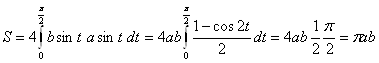

Вычисление объемов тел.

1. Вычисление объемов тел по площадям параллельных сечений.

Пусть требуется вычислить объем некоторого тела V по известным площадям сечений этого тела плоскостями, перпендикулярными прямой OX, проведенными через любую точку x отрезка [a, b] прямой OX.

Применим метод дифференциалов. Считая элементарный объем , над отрезком объемом прямого кругового цилиндра с площадью основания и высотой , получим . Интегрируя и применяя формулу Ньютона – Лейбница, получим

.

2. Вычисление объемов тел вращения.

Пусть требуется вычислить Объем тела вращения вокруг оси OX.

Тогда .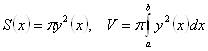

Аналогично, Объем тела вращения вокруг оси OY, если функция задана в виде , можно вычислить по формуле .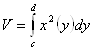

Если функция задана в виде и требуется определить объем тела вращения вокруг оси OY, то формулу для вычисления объема можно получить следующим образом.

Переходя к дифференциалу и пренебрегая квадратичными членами, имеем . Интегрируя и применяя формулу Ньютона – Лейбница, имеем .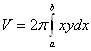

Пример. Вычислить объем шара .

Пример. Вычислить объем прямого кругового конуса, ограниченного поверхностью И плоскостью .

Вычислим объем, как объем тела вращения, образованного вращением вокруг оси OZ прямоугольного треугольника в плоскости OXZ, катеты которого лежат на оси OZ и прямой z = H, а гипотенуза лежит на прямой .

Выражая x через z, получим .

Искомый объем можно посчитать как разность объемов прямого кругового цилиндра С высотой H и тела, вращения, ограниченного цилиндрической, конической поверхностями и плоскостью OXY

.

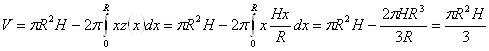Вычисление длины дуги.

Для того, чтобы получить формулы для вычисления длины дуги, вспомним выведенные в 1 семестре формулы для дифференциала длины дуги.

Если дуга представляет собой график непрерывно дифференцируемой функции , дифференциал длины дуги можно вычислить по формуле

. Поэтому

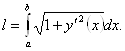
Если гладкая дуга задана параметрически , то

. Поэтому .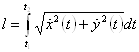

Если дуга задана в полярной системе координат, то

. Поэтому .

Пример. Вычислить длину дуги графика функции, . .

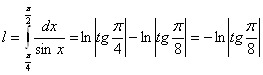Пример. Вычислить длину кардиоиды .

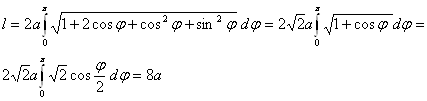
Пример. Вычислить длину одной арки циклоиды. .

.

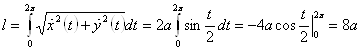Вычисление площади поверхности вращения.

Пусть гладкая дуга представляет собой график непрерывно дифференцируемой функции . Эта дуга вращается вокруг оси OX, описывая некоторую поверхность. Требуется определить площадь этой поверхности.

Считая элемент поверхности боковой поверхностью усеченного конуса, высотой которого является отрезок , получим . Выделяя здесь линейную часть, пренебрегая квадратичным членом от дифференциала , получаем . Интегрируя и применяя формулу Ньютона – Лейбница, получим

.

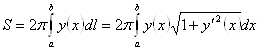Если функция задана параметрически или в полярной системе координат, то в этой формуле производится соответствующая замена переменной, формулы для дифференциала длины дуги Приведены выше.

Пример. Дуга графика функции Вращается вокруг оси OX, образуя «ведерко». Можно ли налить в это ведерко определенное количество краски так, чтобы окрасить боковую поверхность ведерка?

Во-первых, определим, конечен ли объем ведерка.

, интеграл сходится, объем конечен. Ведерко будет окрашено, если будет окрашена каждая точка поверхности, т. е. в том случае, когда боковая поверхность ведерка будет конечна.

. Так как А интеграл Расходится, то по первому признаку сравнения будет расходиться и интеграл . Следовательно, боковая поверхность имеет бесконечную площадь, и боковую поверхность ведерка окрасить не удастся.

< Предыдущая		Следующая >