06. Лекция 6. Формула Ньютона – Лейбница
Интеграл с переменным верхним пределом.
Определенный интеграл представляет собой функцию пределов интегрирования. Это ясно даже из геометрической интерпретации интеграла как площади криволинейной трапеции. Изменяя пределы интегрирования, мы изменяем основание трапеции, изменяя тем самым ее площадь.
Рассмотрим интеграл как функцию верхнего предела интегрирования – Интеграл с переменным верхним пределом  . Переменная интегрирования по свойству 9 определенного интеграла – «немая переменная», ее можно заменить z или t или как - либо еще. Никакого отношения к верхнему пределу интегрирования она не имеет.
. Переменная интегрирования по свойству 9 определенного интеграла – «немая переменная», ее можно заменить z или t или как - либо еще. Никакого отношения к верхнему пределу интегрирования она не имеет.
Теорема о производной интеграла по переменному верхнему пределу (основная теорема математического анализа)
Пусть функция ![]() Непрерывна на отрезке
Непрерывна на отрезке ![]() , пусть
, пусть ![]() . Тогда
. Тогда ![]() .
.
Доказательство. 
![]() .
.
При доказательстве мы воспользовались теоремой о среднем  И непрерывностью функции
И непрерывностью функции ![]() .
.
Формула Ньютона – Лейбница.
Пусть функция ![]() Непрерывна на отрезке
Непрерывна на отрезке ![]() - некоторая первообразная функции
- некоторая первообразная функции ![]() . Тогда
. Тогда 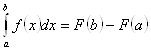 .
.
Доказательство. Из теоремы о производной интеграла по переменному верхнему пределу следует, что ![]() , т. е.
, т. е. ![]() - первообразная для функции
- первообразная для функции ![]() . По теоремам о первообразных две первообразных отличаются на константу т. е.
. По теоремам о первообразных две первообразных отличаются на константу т. е. ![]() Но
Но ![]() (свойство 4 определенного интеграла), поэтому
(свойство 4 определенного интеграла), поэтому ![]() . Тогда
. Тогда 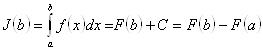 . Следовательно,
. Следовательно,  .
.
Формула Ньютона – Лейбница - это одна из немногих формул - связок, связывающих различные разделы математики воедино. Если бы не было формулы Ньютона – Лейбница, то неопределенные интегралы не нашли бы приложения, а определенные интегралы нельзя было бы вычислить аналитически. Именно эта формула делает интегральное исчисление важнейшим инструментом исследования процессов. Любой процесс описывается дифференциальными или интегральными уравнениями, а они решаются в интегралах.
Мы встречались с такими формулами или теоремами – связками. Например, теорема о связи функции, ее предела и бесконечно малой связывает бесконечно малые и пределы. Теорема Ферма и ее следствия – теоремы о средних значениях связывают дифференциальное исчисление и теорию экстремума. В дальнейшем мы тоже будем встречаться с теоремами – связками, они всегда играют фундаментальную роль, например теоремы Остроградского – Гаусса и Стокса в векторном анализе.
Методы вычисления определенного интеграла.
Методы вычисления остаются теми же, что и методы вычисления неопределенного интеграла, но разница есть. В неопределенном интеграле, делая замену переменной, надо затем возвратиться к исходной функции, в определенном интеграле этого делать не нужно, при замене пересчитываются и пределы интегрирования для новой переменной. Определенный интеграл при постоянных пределах интегрирования – число и все равно, в каких переменных считать это число. Но требование взаимной однозначности функции – замены и в определенном интеграле сохраняется, просто оно маскируется условиями теоремы о замены переменной.
Метод замены переменной.
Пусть
1) ![]() непрерывны при
непрерывны при ![]() ,
,
2) значения ![]() ,
, ![]() не выходят за границы
не выходят за границы ![]() ,
,
3) ![]() ,
,
Тогда 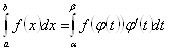
Доказательство. 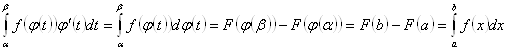 .
.
Пример 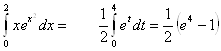 .
.
![]()
Упражнение. Найдите ошибки в применении теоремы о замене переменной.

![]()
Метод интегрирования по частям.
Пусть функции ![]() Непрерывны на
Непрерывны на ![]() . Тогда
. Тогда
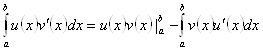
Доказательство остается тем же, что для неопределенного интеграла, только интегрирование проводится в пределах от a до b.
Интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат.
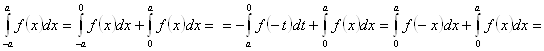
![]()
 , Так как
, Так как
![]() .
.
Интегрирование периодических функций на отрезке длины, кратной периоду.
Два свойства периодических функций.
1) Если ![]() - периодическая функция с периодом T, то
- периодическая функция с периодом T, то ![]() - периодическая функция с периодом
- периодическая функция с периодом ![]() .
.
Доказательство. ![]() .
.
Поэтому период ![]() равен
равен ![]() , период
, период ![]() равен
равен ![]() И т. д.
И т. д.
2) Если ![]() - периодическая функция с периодом T, то
- периодическая функция с периодом T, то

Доказательство. 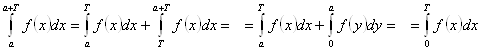
![]()
![]()
Поэтому интеграл от периодической функции на отрезке, длиной равной периоду, можно вычислять на любом таком отрезке, результат будет тем же самым.
Заметим, что 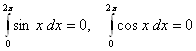 . Поэтому, например,
. Поэтому, например,  .
.
Когда встречаются интегралы от синусов и косинусов на отрезке длины, кратной периоду, то такие интегралы вычислять не стоит, они равны нулю.
| < Предыдущая | Следующая > |
|---|