05. Лекция 5. Определенный интеграл
Задача о площади криволинейной трапеции.
Рассмотрим криволинейную трапецию, образованную отрезком ![]() оси OX (основание трапеции), прямыми
оси OX (основание трапеции), прямыми ![]() (на них лежат боковые
(на них лежат боковые
Стороны трапеции) и графиком функции ![]() . Так как график функции – кривая линия, то такая трапеция называется криволинейной
. Так как график функции – кривая линия, то такая трапеция называется криволинейной
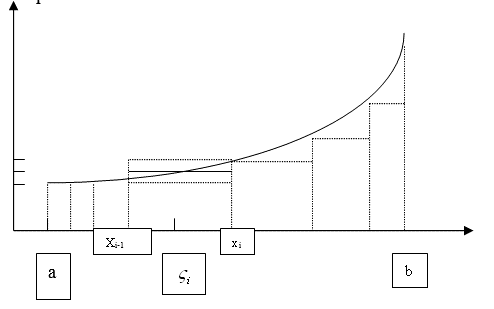
Устроим разбиение отрезка ![]() точками
точками ![]() . Обозначим
. Обозначим ![]() . На каждом отрезке
. На каждом отрезке ![]() отметим точку
отметим точку ![]() . Вычислим
. Вычислим ![]() . Обозначим
. Обозначим ![]() - площадь части криволинейной трапеции над отрезком
- площадь части криволинейной трапеции над отрезком ![]() , S – площадь всей криволинейной трапеции. Тогда
, S – площадь всей криволинейной трапеции. Тогда
![]() Пусть функция
Пусть функция ![]() непрерывна на каждом отрезке
непрерывна на каждом отрезке ![]() . По второй теореме Вейерштрасса выполняется неравенство
. По второй теореме Вейерштрасса выполняется неравенство ![]() , где
, где ![]() - нижняя и верхняя грани функции на отрезке
- нижняя и верхняя грани функции на отрезке ![]() . Тогда
. Тогда
![]()
Сумма ![]() называется Интегральной суммой, Суммы
называется Интегральной суммой, Суммы ![]() ,
, ![]() Называются соответственно нижней и верхней суммами Дарбу.
Называются соответственно нижней и верхней суммами Дарбу.
Будем измельчать разбиение так, чтобы ![]() . Если существует предел интегральных сумм при неограниченном измельчении разбиения, то он называется определенным интегралом (по Риману) от функции
. Если существует предел интегральных сумм при неограниченном измельчении разбиения, то он называется определенным интегралом (по Риману) от функции ![]() по отрезку
по отрезку ![]() :
: 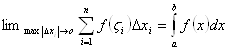 .
.
Если существуют пределы нижней и верхней сумм Дарбу при неограниченном измельчении разбиения, то они называются нижним ![]() И верхним
И верхним ![]() Интегралами Дарбу.
Интегралами Дарбу.
Критерий существования определенного интеграла. Для того, чтобы существовал определенный интеграл по Риману 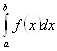 , необходимо и достаточно, чтобы существовали и были равны нижний и верхний интегралы Дарбу.
, необходимо и достаточно, чтобы существовали и были равны нижний и верхний интегралы Дарбу.
Следствие. Если определенный интеграл существует как предел интегральных сумм, то он не зависит
- От выбора разбиения, лишь бы ![]() .
.
- От выбора отмеченных точек ![]() На элементах разбиения
На элементах разбиения
- От способа измельчения разбиения, лишь бы ![]() .
.
Поэтому (Критерий Римана) для интегрируемости по Риману ограниченной на отрезке функции необходимо и достаточно, чтобы существовало некоторое конкретное разбиение отрезка, на котором ![]() для любого
для любого ![]() .
.
Теорема. Если функция непрерывна на отрезке, то она интегрируема на этом отрезке.
Теорема. Если функция кусочно непрерывна на отрезке (имеет на нем не более конечного числа разрывов первого рода), то она интегрируема на этом отрезке.
Мы пришли к определенному интегралу от задачи о площади криволинейной трапеции. Если функция принимает на отрезке неотрицательные значения, то Определенный интеграл можно интерпретировать как площадь под графиком функции. В этом состоит Геометрический смысл определенного интеграла.
К понятию интеграла можно придти и от других задач. Например, от задачи О работе переменной по величине силы, не меняющей направления на прямолинейном пути, От задачи о массе отрезка, плотность которого меняется от точки к точке, от задачи о пути тела, движущегося прямолинейно с переменной скоростью. Фактически, все эти задачи формально сводятся к задаче о площади криволинейной трапеции. В задаче о работе силы по оси ординат откладываются значения скалярного произведения вектора силы в данной точке x отрезка на орт оси OX. В задаче о массе отрезка по оси ординат откладываются значения переменной плотности. В задаче о пути, пройденном телом, по оси ординат откладывается величина скорости тела в данной точке.
К схеме определенного интеграла сводится любая задача вычисления некоторой величины, аддитивно зависящей от множества, т. е. величины I, удовлетворяющей соотношению ![]() , где А, В – отрезки оси OX (в общем случае определенного интеграла по некоторому множеству А, В – некоторые множества). В качестве таких величин можно выбрать длину отрезка, длину кривой, площадь поверхности, объем пространственного тела, массу указанных множеств и т. д.
, где А, В – отрезки оси OX (в общем случае определенного интеграла по некоторому множеству А, В – некоторые множества). В качестве таких величин можно выбрать длину отрезка, длину кривой, площадь поверхности, объем пространственного тела, массу указанных множеств и т. д.
Свойства определенного интеграла.
1. Свойства линейности
а) суперпозиции ![]() ,
,
б) однородности ![]()
Вообще говоря, свойствами линейности обладают все линейные операции (дифференцирование, интегрирование, проектирование и т. д.)
2. Свойство аддитивности (по множеству)
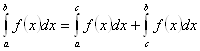
Доказательство. Пусть ![]() . Выберем разбиение так, чтобы точка с была границей элемента разбиения
. Выберем разбиение так, чтобы точка с была границей элемента разбиения ![]() . Это возможно (следствие). Составим интегральную сумму
. Это возможно (следствие). Составим интегральную сумму ![]() . Будем измельчать разбиение, сохраняя точку с границей элемента разбиения. Это возможно (следствие). Тогда предел при
. Будем измельчать разбиение, сохраняя точку с границей элемента разбиения. Это возможно (следствие). Тогда предел при ![]() Левой части равенства интегральных сумм равен
Левой части равенства интегральных сумм равен  , первого слагаемого правой части
, первого слагаемого правой части 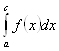 , второго слагаемого правой части
, второго слагаемого правой части 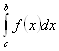 .
.
3. 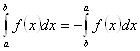 (свойство «ориентируемости» множества).
(свойство «ориентируемости» множества).
Составляя интегральную сумму для интеграла в правой части равенства, заметим, что элемент разбиения надо проходить в другом направлении, от конца отрезка к началу. Поэтому для этого интеграла интегральная сумма будет
![]() -
- ![]() . Переходя к пределу при измельчении разбиения, получим
. Переходя к пределу при измельчении разбиения, получим 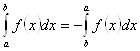 .
.
4. 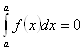 . Это постулируется, но, вообще говоря, это и очевидно.
. Это постулируется, но, вообще говоря, это и очевидно.
5. 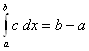 .
.
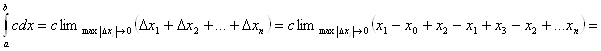
![]() .
.
6. Если на отрезке ![]() , то
, то 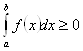 .
.
Так как ![]() на отрезке, то
на отрезке, то ![]() . Переходя к пределу, получим
. Переходя к пределу, получим 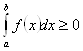 .
.
7. Если на отрезке ![]() , то
, то 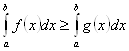 .
.
Так как ![]() на отрезке, то
на отрезке, то ![]() . Переходя к пределу, получим
. Переходя к пределу, получим  .
.
8. 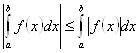
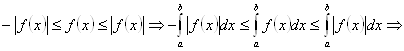
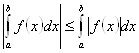 .
.
9. 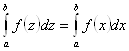 (переменная интегрирования – «немая» переменная, ее можно изменить, она не несет в себе самостоятельного смысла)
(переменная интегрирования – «немая» переменная, ее можно изменить, она не несет в себе самостоятельного смысла)
Определенный интеграл является функцией своих пределов, при фиксированных пределах интегрирования это – число. Он определен своими пределами. Поэтому он и называется определенным.
Теорема об оценке определенного интеграла.
Пусть на отрезке ![]()
![]() И функция
И функция ![]() интегрируема на отрезке. Тогда
интегрируема на отрезке. Тогда
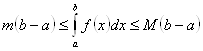
Доказательство. Интегрируя по свойству 7 неравенство ![]() , с учетом свойства 5 получаем требуемое утверждение.
, с учетом свойства 5 получаем требуемое утверждение.
Теорема об оценке полезна, когда интеграл вычислить трудно или вообще невозможно, но приблизительно оценить его необходимо. Это часто встречается в инженерной практике.
Пример. ![]() . Такой интеграл «не берется». Но
. Такой интеграл «не берется». Но ![]() на отрезке
на отрезке ![]() . Поэтому, учитывая четность подынтегральной функции, получим
. Поэтому, учитывая четность подынтегральной функции, получим ![]()
![]()
![]() . Конечно, это – очень грубая оценка, более точную оценку можно получить, применяя методы численного интегрирования.
. Конечно, это – очень грубая оценка, более точную оценку можно получить, применяя методы численного интегрирования.
Теорема о среднем значении определенного интеграла («теорема о среднем»).
Пусть функция ![]() непрерывна на отрезке
непрерывна на отрезке ![]() . Тогда существует
. Тогда существует ![]() , что
, что 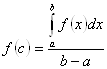 (или
(или 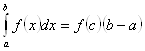 ).
).
Геометрически, смысл этого соотношения состоит в том, что площадь криволинейной трапеции равна площади прямоугольника с тем же основанием и высотой ![]() .
.
Доказательство. По второй теореме Вейерштрасса функция, непрерывная на отрезке, достигает на нем своей верхней ![]() и нижней
и нижней ![]() грани. По теореме об оценке
грани. По теореме об оценке 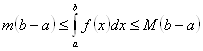 , откуда, деля на
, откуда, деля на ![]() , получим
, получим
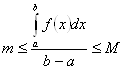 . По второй теореме Больцано – Коши функция, непрерывная на отрезке, принимает на нем все промежуточные значения между m и M. В частности, существует и такая точка
. По второй теореме Больцано – Коши функция, непрерывная на отрезке, принимает на нем все промежуточные значения между m и M. В частности, существует и такая точка ![]() , в которой функция принимает свое промежуточное значение
, в которой функция принимает свое промежуточное значение 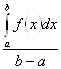 , т. е.
, т. е. 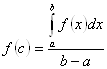
| < Предыдущая | Следующая > |
|---|