04. Лекция 4. Интегрирование иррациональных и тригонометрических функций

Интегрирование рациональных функций от тригонометрических функций.

1. , где R( ) – рациональная функция своих аргументов.

Такие интегралы всегда можно взять Универсальной тригонометрической подстановкой (лекция 1)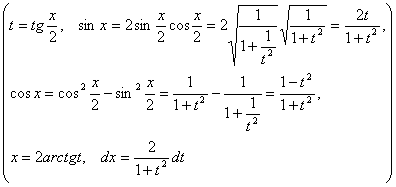

2. .

А) Если нечетна по sin x, то делают подстановку t = cos x.

Б) Если нечетна по cos x, то делают подстановку t = sin x.

В) Если не меняет знака при изменении знака sin x или cos x, то делают подстановку t = tg x.

Пример. . Здесь мы имеем случай В). Подстановкой этот интеграл сводится к интегралу .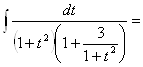

3. Интегралы

Сводятся к табличным интегралам от синуса и косинуса, если преобразовать произведение тригонометрических функций в сумму по формулам

Пример.

4. Интегралы вида

A) Если m или n – нечетное положительное число, то sin x или cos x вносят под дифференциал.

Пример.

B) Если m, n – четные положительные числа, то применяют формулы удвоения аргумента

Пример.

C) , где m – целое положительное число, берутся с использованием формул .

Пример.

= -

D) В общем случае интегралы вида вычисляются по рекуррентным формулам с использованием основного тригонометрического тождества.

Пример.

= .

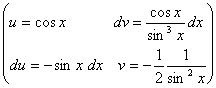
Интегрирование иррациональных функций.

Каких-либо общих методов интегрирования для всего класса иррациональных функций неизвестно, да и вряд ли такие методы можно придумать.

Общая идея состоит в том, чтобы придумать рационализирующую подстановку, т. е. найти такую замену переменных, чтобы в новых переменных интеграл был бы интегралом от рациональной функции. А, как показано на прошлой лекции, интегралы от рациональных функций всегда можно взять.

Ниже приводятся некоторые интегралы, для которых известны рационализирующие подстановки.

1. 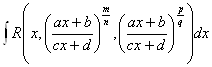, где R( ) – рациональная функция аргументов. Рационализирующая подстановка , где .

Пример. - интеграл от рациональной функции, если взять .

2. . Этот интеграл можно представить в виде = , а затем искать коэффициенты полинома n-1 степени и константу, дифференцируя обе части, приводя дроби к общему знаменателю и приравнивая коэффициенты при одинаковых степенях переменной.

Пример. .

Дифференцируем обе части

.

Приводим к общему знаменателю

. Приравнивая коэффициенты при одинаковых степенях, получаем . Теперь, выделяя полный квадрат, получаем в правой части разложения «длинный логарифм»:

.

3. В интегралах вида рационализирующая подстановка .

Пример. . Применяем подстановку .

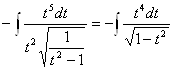= . Это интеграл, рассмотренный выше в п.2.

4. Дифференциальный бином. , где - рациональные числа. Такие интегралы берутся только в трех случаях (условия П. Л.Чебышева):

А) p – целое (подстановкой , где ),

Б)- целое (подстановкой ),

В) - целое (подстановкой).

Пример. Показать, что в интеграле - целое и равно 2. Показать, что подстановка - рационализирующая.

5. Интегралы вида сводятся к одному из трех типов интегралов:

А), для которого рационализирующие подстановки ,

Б) , с подстановками ,

В) , с подстановками .

Упражнение. Вычислить интегралы .

«Неберущиеся» интегралы.

Это интегралы, которые не могут быть вычислены в элементарных функциях. Для таких интегралов приходится вводить специальные символы. Так получается потому, что класс интегралов от элементарных функций шире, чем класс элементарных функций (интегрирование – это переход от частного к общему – обобщение, а дифференцирование – это переход от общего к частному – уточнение).

Примеры. и многие другие интегралы. Для них составляются специальные таблицы, которые можно найти в различных учебниках и справочниках.

< Предыдущая		Следующая >