03. Лекция 3. Интегрирование рациональных функций

Рациональная функция – это отношение двух целых функций – многочленов (полиномов).

Если порядок полинома – числителя ниже порядка полинома – знаменателя, то такая рациональная функция называется Рациональной дробью.

Лемма 1. Если рациональная функция не является рациональной дробью, то ее можно привести к сумме целой части – полинома и рациональной дроби.

Доказательство основано на правиле деления многочленов с остатком, например, на алгоритме деления многочленов «уголком».

Пример. .

Отсюда следует, что .

Поэтому интегрирование рациональной функции сводится к интегрированию многочлена и интегрированию рациональной дроби.

Интеграл от многочлена равен по свойствам линейности интеграла сумме произведений интегралов от степенных функций на постоянные коэффициенты. Интеграл от степенной функции легко вычислить по таблице интегралов.

Разложение рациональной дроби на элементарные.

Полином – знаменатель рациональной дроби может иметь действительный корень Некоторой - ой кратности. Тогда , где многочлен уже не имеет корня . В этом случае из рациональной дроби можно выделить элементарную рациональную дробь вида .

Лемма 2. Пусть - действительный корень - ой кратности полинома – знаменателя рациональной дроби. Тогда

= , где многочлен уже не имеет корня .

Доказательство. Приведем дроби к общему знаменателю и приравняем числители полученных дробей.

. Тогда выражение должно делиться на , т. е. . Этого можно добиться, выбрав .

Следствие 1. В условиях леммы 2 рациональную дробь можно представить в виде

Где не имеет корня .

Доказательство. Применим лемму 2 раз и получим указанное разложение.

Полином – знаменатель рациональной дроби может иметь пару комплексно сопряженных корней - ой кратности. Тогда Причем уже не являются корнями полинома . В этом случае из рациональной дроби тоже можно выделить некоторую элементарную рациональную дробь вида .

Лемма 3. Пусть – знаменатель рациональной дроби Имеет пару комплексно сопряженных корней - ой кратности. Тогда рациональную дробь можно представить в виде

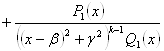= , где уже не являются корнями полинома .

Доказательство. Приведем дроби к общему знаменателю и приравняем числители полученных дробей.

=. Должно делиться как на , так и на . Поэтому

, где =, =

Отсюда имеем систему уравнений для определения констант

Определитель этой системы равен , так как корни комплексные и . Поэтому система имеет единственное решение.

Следствие 2. В условиях леммы 2 рациональную дробь можно представить в виде

= ++ …++ ,

Где уже не являются корнями полинома .

Доказательство. Применяем лемму 3 нужное число раз и получаем искомое разложение.

Теорема. Рациональная функция может быть представлена в виде

=++…+ +…+++ …++ …+,

Где - простой действительный корень , - действительный корень Кратности , - пара комплексно сопряженных корней кратности (комплексно сопряженные корни ), - простая пара комплексно сопряженных корней (корни ).

Доказательство. Применяем к рациональной функции лемму 1, выделяем полином – целую часть , затем по лемме 2, выделяем члены разложения, соответствующие простым и кратным действительным корням. Затем по лемме 3 выделяем члены разложения, соответствующие простым и кратным парам комплексно сопряженных корней. Так как многочлен может иметь корни лишь перечисленных типов, то разложение этим и исчерпывается.

Следствие 3. Задача интегрирования рациональной функции сводится к задачам интегрирования элементарных рациональных дробей четырех типов

1) , 2) , 3) , 4).

Способы вычисления коэффициентов при разложении рациональной дроби на элементарные.

Пример.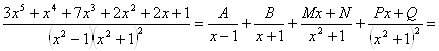

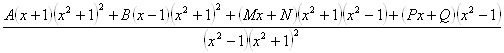
Теперь надо приравнивать многочлены в числителях дробей и определять неизвестные коэффициенты A, B, M, N, P, Q.

Это можно сделать двумя способами.

1 способ – приравнивать коэффициенты при одинаковых степенях переменной, составлять и решать систему уравнений.

X5| 3=A+B+M

X4| 1=A-B+N

X3| 7=2A+2B+P

X2| 2=2A-2B+Q Решение системы A=2, B=1, M=N=Q=0, P=1.

X |2=A+B-N-P

1 |1=A-B-N-Q

2 способ – задавать значения неизвестной, вычислять значения числителей и составлять систему уравнений.

X=1 | 16=8A

X= -1| -8=-8B

X=0 | 1=A-B-N-P

X=2 | 181=75A-25B+30M+15N+6P+3Q

X=-2 | -96= -25A-75B-30M+15N-6P+3Q

X=-3 | -824= -200A –400B-240M –80N –24P+8Q

Решая эту систему уравнений, получим то же решение A=2, B=1, M=N=Q=0, P=1.

Какой способ применять – зависит от того, где получается более простая и удобная для решения система уравнений.

В данном примере вторая система сложнее первой.

Интегрирование элементарных рациональных дробей четырех типов.

1) ,

3) =

(пример рассмотрен во второй лекции). Для того, чтобы вычислить интеграл от дроби в п.3, достаточно в соответствующем примере второй лекции обозначить коэффициенты другими буквами.

4) ==

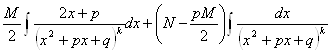, где .

Вычислим интеграл .

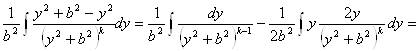
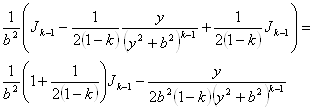
По этой рекуррентной формуле можно последовательно вычислять интегралы при различных , предварительно вычислив

Таким образом, показано, что все четыре типа элементарных рациональных дробей интегрируемы. Следовательно, Класс рациональных функций представляет собой класс интегрируемых функций.

При интегрировании конкретных рациональных функций выделяют целую часть и раскладывают рациональную дробь на элементарные. Затем интегрируют элементарные рациональные дроби.

Пример.

Составляем и решаем систему уравнений относительно неопределенных коэффициентов (первый способ определения коэффициентов)

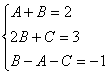Получим

Можно воспользоваться и вторым способом определения коэффициентов.

X=0 | -1 = B-A-C

X=1 | 4 = A+B+2B+C+B-A-C= 4B

X=-1| -2 = A+B-2B-C+B-A-C= -2C. Отсюда C=1, B=1, A=1.

Вторая система проще, чем первая.

Теперь интегрируем сумму элементарных дробей.

Метод Остроградского.

Если знаменатель рациональной дроби содержит пары комплексно сопряженных корней большой кратности, то удобно применять метод Остроградского. Он состоит в следующем: вычисляют . Затем интеграл представляют в виде

, где степень на единицу меньше степени , а степень на единицу меньше степени . Коэффициенты полиномов , определяются при дифференцировании левой и правой частей и приравнивания коэффициентов при равных степенях x.

< Предыдущая		Следующая >