6.4. Асимптоты

Определение 1. Прямая называется Наклонной асимптотой функции при , если существуют числа и такие, что.

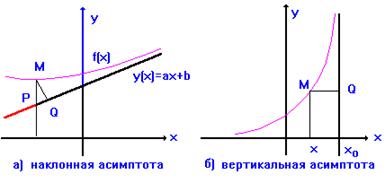
Аналогично определяется наклонная асимптота при .

Геометрически асимптота представляет собой прямую к которой неограниченно приближается функция при :

при .

Для нахождения наклонной асимптоты следует определить величины и в уравнении асимптоты - прямой . Разделим разность на и устремим , получим

.

Выразим из равенства , получим .

В частности, если , то асимптота называется Горизонтальной, ее уравнение есть прямая параллельная оси .

Пример 1. Найти наклонные асимптоты функции

.

,

.

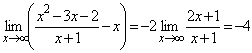Искомое уравнение асимптоты имеет вид .

Определение 2. Прямая называется Вертикальной асимптотой функции при , если

.

Пример 2. Функция, рассмотренная в примере 1, имеет вертикаль-ную асимптоту , т. к.

.

< Предыдущая		Следующая >