6.2. Условия наличия экстремумов функции. Задача исследования функции на экстремум

Необходимое условие экстремума.

Если точка является точкой экстремума функции , то либо , либо не существует .

Доказательство. Если в точке экстремума существует производная , то по теореме Ферма .

Замечание. Условие не является достаточным условием наличия экстремума. Так, у функции производная , но точка не является точкой экстремума.

Пример. Функция имеет минимум в точке , хотя у нее не существует производной в точке , т. к. .

Первое достаточное условие экстремума.

Пусть функция дифференцируема в некоторой окрест-ности точки . Если ее производная меняет знак при переходе через точку , то является точкой экстремума, причем точкой максимума, если производная меняет знак с “+” на “-” и точкой минимума, если с “-” на “+”.

Доказательство. По теореме Лагранжа

.

При имеем слева от точки . При имеем справа от точки , т. е. точка является точкой строгого максимума.

Аналогично рассматривается случай минимума.

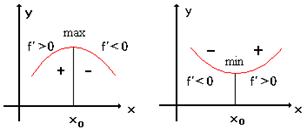
В задаче исследования функции на экстремум функции сначала следует определить критические и стационарные точки, а потом использовать достаточный признак экстремума.

Пример 1. Исследовать на экстремум функцию .

Найдем . Производная существует на всем мно-жестве определения функции, поэтому остается найти только стационарные точки, в которых . Из уравнения находим - единственная стационарная точка. Слева от точки имеем , а справа . Поэтому есть точка максимума, причем

Второе достаточное условие экстремума.

Пусть функция дифференцируема раз в точке и , но . Тогда, если (четное число), то является точкой максимума при и точкой минимума при . Если же (нечетное число), то является точкой возрастания функции при и убывания при .

Следствие 1. Пусть функция дифференцируема дваж-ды в точке . Если , то является точкой экстремума, а именно, точкой максимума, если и точкой минимума, если .

Следствие 2. Пусть функция дифференцируема в точке . Если , то является возрастания функции, а если - точкой убывания.

Доказательство. Запишем формулу Тейлора -го порядка для функции в окрестности точки и учтем, что , получим

.

Если , то знак не зависит от знака , и поэтому знак сохраняется при переходе через точку , а именно , если - максимум и , если - минимум.

Если , то знак зависит от знака , а т. к. последний меняется при переходе через точку , то Не является точкой экстремума. Далее, при переходе через точку величина меняет знак с “-” на “+”; при величина Меняет знак с “-” на “+” и точка является точкой возрастания функции ; при величина Меняет знак с “+” на “-” и является точкой убывания.

Пример 2. Функция имеет стационарную точку . Найдем производные . Подставим точку во вторую производную, получим . Поэтому является точкой максимума.

< Предыдущая		Следующая >