5.3. Формула Тейлора
Теорема. Пусть функция ![]() определена в некоторой окрестности
определена в некоторой окрестности ![]() точки
точки ![]() дифференцируема
дифференцируема ![]() раз в точке
раз в точке ![]() . Тогда имеет место, притом единственное, разложение в окрестности
. Тогда имеет место, притом единственное, разложение в окрестности ![]() точки
точки ![]() функции
функции ![]() в сумму
в сумму
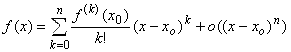 . (1)
. (1)
Здесь ![]() есть бесконечно малая более высокого порядка малости по сравнению с
есть бесконечно малая более высокого порядка малости по сравнению с ![]() .
.
Разложение (1) в сумму называется Формулой Тейлора.
Доказательство. Предположим, что существует многочлен ![]() приближающийся к функции
приближающийся к функции ![]()
![]() , (2)
, (2)
![]() . (3)
. (3)
При ![]() имеем
имеем ![]() .
.
Дифференцируем (3) последовательно ![]() раз и каждый раз полагаем
раз и каждый раз полагаем ![]() , получим
, получим
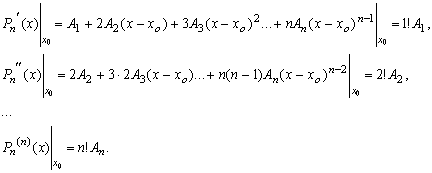 Сопоставляя с (2) и (3), находим
Сопоставляя с (2) и (3), находим
![]() ,
,
Что соответствует (1).
Обозначим остаточный член в формуле Тейлора ![]() . Остается показать, что
. Остается показать, что ![]() при
при ![]() Для этого заметим, что
Для этого заметим, что
![]() .
.
Это означает, что

Следствие. Полагая в формуле Тейлора ![]() , получим Формулу Маклорена
, получим Формулу Маклорена
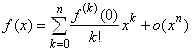 . (4)
. (4)
Применяя формулу Маклорена к основным элементарным функциям, получим следующие разложения
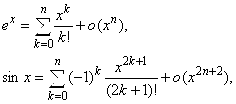

Для вывода каждой из этих формул следует найти коэффициенты ![]() . Например, для функции
. Например, для функции ![]() имеем
имеем ![]() ; для функции
; для функции ![]() имеем
имеем
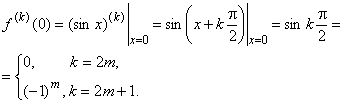
Остаточный член ![]() в формуле (1) часто называют Формой Пеано. Его можно записать в форме Лагранжа
в формуле (1) часто называют Формой Пеано. Его можно записать в форме Лагранжа
![]() . (5)
. (5)
Нестрого эту форму можно получить непосредственно из формулы Тейлора, распространив последнюю на случай ![]() . Тогда
. Тогда ![]() -й член разложения имеет вид
-й член разложения имеет вид ![]() , а остаточный член учесть заменой точки
, а остаточный член учесть заменой точки ![]() на точку
на точку ![]() .
.
Пример.
Используя формулы Маклорена для простейших функций, написать первые N членов разложения Маклорена для функции
1.![]() .
.
В разложении ![]() положим
положим ![]()
 .
.
2. ![]() . Представим
. Представим ![]() и используем разложение
и используем разложение ![]() :
: 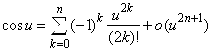
![]()
 .
.
| < Предыдущая | Следующая > |
|---|