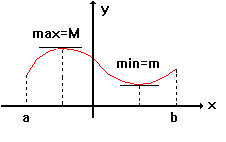5.1. Применение производной. Теоремы о среднем

Определение. Функция имеет в точке Локальный максимум (Минимум), если в которой выполняется неравенство . Если имеет место строгое неравенство , то Максимум (Минимум) называется Строгим максимумом (Минимумом).

Локальные максимумы и минимумы функции называются Экстремумами функции.

Теорема Ферма.

Если функция дифференцируема в точке и в этой точке имеется экстремум, то .

Геометрический смысл теоремы Ферма.

Если есть точка локального экстремума функции , то касательная к графику в точке параллельна оси .

Доказательство. Пусть точка есть точка локального максимума функции , тогда выполняется неравенство или . При имеем , а при имеем В пределе при имеем и . По предположению .

Теорема Ролля.

Пусть функция

1) непрерывна на отрезке ;

2) дифференцируема на интервале ;

3) .

Тогда , в которой .

Геометрический смысл теоремы Ролля

У графика дифференцируе-мой функции на интервале , и принима-ющей на концах одинаковые значения, всегда найдется точка в которой касательная параллельна оси .

Доказательство. Непрерывная на отрезке функция всегда ограничена на этом отрезке. Отсюда, : . Поскольку , то или . По теореме Ферма .

Если , то и .

Замечание 1. По условию теоремы точка не обязательно должна быть единственной.

Теорема Лагранжа.

Пусть функция удовлетворяет условиям 1) и 2) теоремы Ролля. Тогда , в которой выполняется равен-ство

Доказательство. Рассмотрим функцию и определим число так, чтобы , т. е. . Для функции выполнены условия 1), 2) и 3) теоремы Ролля, поэтому , в которой . Подставим это значение в равенство , получим формулу Лагранжа.

Геометрический смысл теоремы Лагранжа

У графика дифференцируе-мой функции на интервале всегда най-дется точка , в которой ка-сательная параллельна хорде : , а .

Откуда следует формула Лагранжа.

Замечание 2. Так же как в теореме Ролля точка не обязательно должна быть единственной.

Формы записи формулы Лагранжа.

1) Положим в формуле Лагранжа . Тогда имеем

. (1)

2) Положим в формуле (1) , получим

. (2)

Эту формулу называют Формулой конечных приращений Лагран-жа и часто записывают в виде

.

Теорема Коши.

Пусть функции и удовлетворяют условиям 1) и 2) теоремы Ролля и условию 3) . Тогда в которой

.

Доказательство. Рассмотрим функцию и определим число так, чтобы , т. е. . Для функции выполнены условия 1), 2) и 3) теоремы Ролля, поэтому , в которой . Подставим это значение в равенство , получим формулу Коши.

Следствие 1. Формула Лагранжа является частным случаем формулы Коши при

Следствие 2. Теорема Лопиталя.

Если функции и удовлетворяют условиям 1), 2) теоремы Ролля и

, то . (3)

Если последний предел не имеет неопределенность, то формулу записывают в виде

(4)

И часто называют формулой Лопиталя.

Доказательство. Пусть функции удовлетворяет условиям 1) и 2) теоремы Ролля на отрезке . По теореме Коши это означает, что , в которой , где . Перейдем к пределу в равенстве при , получим формулы (3), (4).

Замечание. Теорема Лопиталя остается справедливой, если , а также в случае . Доказательство проводится аналогично, если рассмотреть вместо функций функции .

< Предыдущая		Следующая >