4.09. Производные и дифференциалы высших порядков
Если функция ![]() имеет производную на некотором множестве
имеет производную на некотором множестве ![]() , то на этом множестве определена функция
, то на этом множестве определена функция ![]() . Если эта функция дифференцируема в некоторой точке
. Если эта функция дифференцируема в некоторой точке ![]() , тогда у нее существует производная, которая называется Второй производной или Производной второго порядка и обозначается:
, тогда у нее существует производная, которая называется Второй производной или Производной второго порядка и обозначается:
![]() .
.
Аналогично определяется производная любого порядка ![]() , а именно, по индукции
, а именно, по индукции ![]() .
.
Примеры:
1. ![]()
![]()
![]()
![]() и т. д.
и т. д.
Аналогично доказывается формула для косинуса.
2. ![]()
![]()
![]() и т. д.
и т. д.
Теорема. Пусть функции ![]() и
и ![]()
![]() раз дифференцируемы в некоторой точке
раз дифференцируемы в некоторой точке ![]() , тогда существуют производные
, тогда существуют производные ![]() -го порядка функций
-го порядка функций ![]() в этой точке , причем
в этой точке , причем

Где ![]() - число сочетаний из
- число сочетаний из ![]() элементов по
элементов по ![]() .
.
Вторая из формул носит название формулы Лейбница.
Доказательство теоремы проводится по индукции. При ![]() равенства очевидны. Предположим, что они выполняются при
равенства очевидны. Предположим, что они выполняются при ![]() и докажем для случая
и докажем для случая ![]() .
.
![]() .
.
Аналогично рассматривается доказательство формулы Лейбница
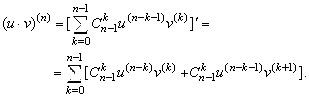
Перепишем равенство в виде
![]()
Во второй сумме обозначим ![]()

Учтем, что ![]()
![]()
Формально член ![]() записан при
записан при ![]() , а член
, а член ![]() при
при ![]() . Учитывая, что
. Учитывая, что ![]() , получим
, получим
![]() .
.
Следствие.![]() .
.
Пусть функция ![]() дифференцируема на некотором множестве
дифференцируема на некотором множестве ![]() , тогда у нее существует дифференциал
, тогда у нее существует дифференциал ![]() , который рассмотрим как функцию только
, который рассмотрим как функцию только ![]() (т. е.
(т. е. ![]() фиксировано). Тогда,
фиксировано). Тогда,
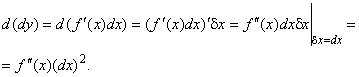
Дифференциал от первого дифференциала ![]() в некоторой точке
в некоторой точке ![]()
![]() называется Вторым дифференциалом или Дифференциалом Второго порядка в этой точке и обозначается
называется Вторым дифференциалом или Дифференциалом Второго порядка в этой точке и обозначается ![]() . Итак,
. Итак, ![]() , откуда следует обозначе-ние второй производной
, откуда следует обозначе-ние второй производной ![]()
Аналогично определяется дифференциал ![]() любого порядка
любого порядка ![]() а именно,
а именно,
![]() .
.
Отсюда следует обозначение ![]() Й производной
Й производной ![]()
Свойства дифференциалов высших порядков:
![]()
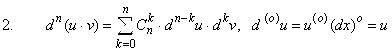 ,
,
![]()
Пример. Вычислить 20-ю производную функции
![]() .
.
Обозначим ![]() и воспользуемся формулой Лейбница
и воспользуемся формулой Лейбница
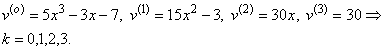
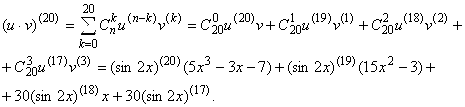 Используем формулы
Используем формулы ![]() ,
, ![]() , получим
, получим
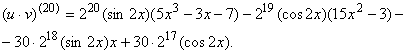
| < Предыдущая | Следующая > |
|---|