4.08. Дифференцирование неявных функций. Логарифмическое дифференцирование

До сих пор мы рассматривали явно заданные функции . Это частный случай более общего вида функций , задаваемых уравнением . Подставим в урав-нение, получим тождество . Последнее дифферен-цируем как сложную функцию и решаем полученное уравнение относительно .

Примеры.

1. Функция задана уравнением .

Считая , дифференцируем левую и правую часть уравнения одновременно

.

2. Функция задана уравнением .

Считая , дифференцируем левую и правую часть уравнения одновременно

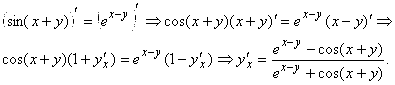
Пусть задана, так называемая "Показательно-степенная" функция . Логарифмируем обе части равенства, получим . Дифференцируем равенство как неявную функцию:

(1)

Примеры.

3. .

4. Аналогично вычисляется производная функции .

Поскольку , то

Таблица производных (продолжение)

6. ,

В §17 выведена производная степенной функции для степени . Прологарифмируем функцию и затем продиф-ференцируем равенство:

.

< Предыдущая		Следующая >