4.07. Производная сложной функции

Теорема. Пусть функция дифференцируема в точке , а функция дифференцируема в точке . Тогда сложная функция дифференцируема в точке , причем

. (1)

Следствие 1. Правило дифференцирования сложной функции

Доказательство. Из дифференцируемости функции в точке следует, что . Разделим равенство на и перейдем к пределу , получим

;

.

Последнее слагаемое равно нулю, поскольку

Следствие 2. Инвариантность формы первого дифференциала относительно преобразования независимой переменной

или .

Умножим равенство (1) на и учтем, что , получим

Следствие 3. Теорема по индукции распространяется на супер-позицию конечного числа функций. Так, для трех функций имеем .

Методика дифференцирования Сложной функции: сначала при-меняются правила дифференцирования к «внешним» арифме-тическим операциям над составляющими функции, затем таблица производных к композициям элементарных функций. Если в композиции встречаются арифметические операции, то приме-няются правила дифференцирования к «внутренним» арифме-тическим операциям и т. д.

Примеры.

1. .

Функция состоит из композиции трех основных элементарных функций и «внутренних» арифметических операций сложения и вычитания.

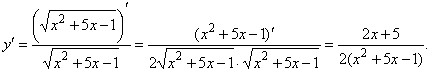
2..

Внешней арифметической операцией является частное, которое состоит из суперпозиций функций. Имеется внутренняя арифме-тическая операция суммы.

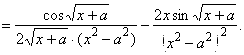
4. , .

При имеем .

При имеем .

5. .

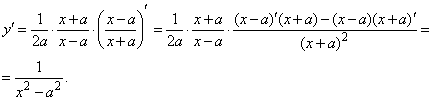6. .

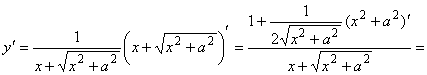
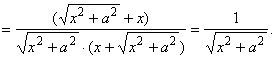
Последние три примера важны при выводе таблицы интегралов.

< Предыдущая		Следующая >