4.06. Производная обратной функции
Теорема. Пусть функция ![]() дифференцируема в точке
дифференцируема в точке ![]() и монотонна в некоторой окрестности
и монотонна в некоторой окрестности ![]() . Тогда обратная функция
. Тогда обратная функция ![]() :
:
1) определена и непрерывна в окрестности ![]()
![]() ,
,
2) дифференцируема в точке ![]() , причем
, причем
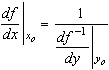 или кратко
или кратко ![]() .
.
Доказательство. Из дифференцируемости функции ![]() сле-дует ее непрерывность в точке
сле-дует ее непрерывность в точке ![]() , а это условие и монотонность обеспечивают существование непрерывной обратной функции
, а это условие и монотонность обеспечивают существование непрерывной обратной функции ![]() в окрестности
в окрестности ![]() . Поэтому, если
. Поэтому, если ![]() , то в силу непрерывности функции
, то в силу непрерывности функции ![]() имеем
имеем ![]() , а в силу ее монотонности при
, а в силу ее монотонности при ![]() следует
следует ![]() . Тогда можно записать
. Тогда можно записать 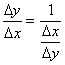 . Перейдем в этом выражении к пределу при
. Перейдем в этом выражении к пределу при ![]() :
:  .
.
Геометрический смысл производной обратной функции.
Построим график дифференцируемой функции ![]() .
.
|
|
Проведем касательную в точке ![]() и обозначим углы, образованные касательной с ося-ми
и обозначим углы, образованные касательной с ося-ми ![]() и
и ![]() , соответственно
, соответственно ![]() и
и ![]() , заметим также, что
, заметим также, что ![]() , тогда,
, тогда,
![]() ,
,
А с другой стороны,
![]() .
.
Итак, производная обратной функции ![]() равна тангенсу угла между касательной к графику в точке
равна тангенсу угла между касательной к графику в точке ![]() и осью ординат.
и осью ординат.
Таблица производных (продолжение)
11.  .
.
Обратной функцией для функции ![]() является
является ![]() . Поэтому
. Поэтому
![]() .
.
12. 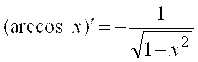 .
.
Обратной функцией для функции ![]() является
является ![]() . Поэтому
. Поэтому
![]() .
.
13.  .
.
Обратной функцией для функции ![]() является
является ![]() . Поэтому
. Поэтому
![]() .
.
14.  .
.
Обратной функцией для функции ![]() является
является ![]() . Поэтому
. Поэтому
![]() .
.
15. 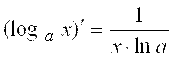 .
.
Обратной функцией для функции ![]() является
является ![]() . Поэтому
. Поэтому
![]() .
.
В частном случае ![]() , имеем
, имеем
16. 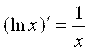 .
.
Дополним таблицу производными от гиперболических функ-ций - гиперболического синуса, косинуса, тангенса и котангенса
![]() .
.
Замечание. Для гиперболических функций существует анало-гичное как для тригонометрических функций - основное “гипербо-лическое” тождество ![]() .
.
17. ![]() .
.
 .
.
18. ![]() .
.
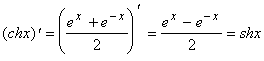 .
.
19.  .
.
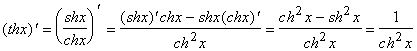 .
.
20.  .
.

| < Предыдущая | Следующая > |
|---|
