4.05. Правила дифференцирования

Теорема. Если функции и дифференцируемы в неко-торой точке , то дифференцируемы функции +, , / (в последнем случае ) в этой точке, причем

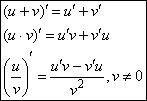
Доказательство. Прежде всего, перепишем приращения функций и в виде

.

Докажем первую формулу. Для этого рассмотрим функцию и найдем ее приращение

Поскольку функции и дифференцируемы, то существует предел и этот предел равен . Следовательно, .

Рассмотрим теперь функцию и найдем ее приращение

Наконец, рассмотрим функцию и найдем ее приращение

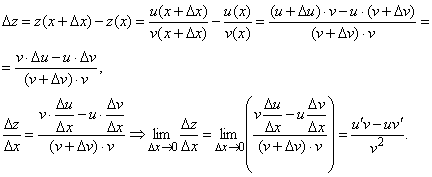При вычислении последнего предела учтена непрерывность функции , т. е. .

Следствие 1. .

Следствие 2. .

Следствие 3. Правила дифференцирования переносятся на дифференциалы функций

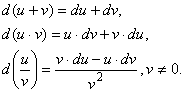
Таблица производных (продолжение)

7. .

Используем правило дифференцирования частного для функции :

8. .

.

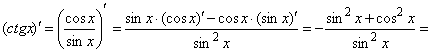
< Предыдущая		Следующая >