4.03. Геометрический смысл производной и дифференциала

Построим график дифференцируемой функции . Выберем произвольно на кривой две точки и .

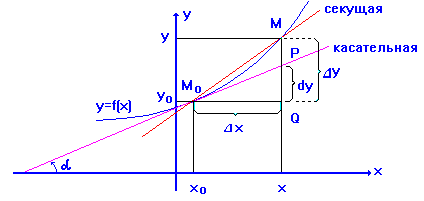
Проведем секущую , ее уравнение имеет вид - угловой коэффициент прямой . Устремим , получим

,

С одной стороны, а с другой стороны при , точка по дуге стремится к точке и секущая переходит в касательную к графику в точке , причем - ее угловой коэффициент. Откуда следует, что

Итак, производная равна тангенсу угла между каса-тельной к графику функции в точке и осью абсцисс .

Из рисунка видно, что

.

Итак, геометрически дифференциал равен линейной части приращения функции в точке . Очевидно, что при .

Из предыдущих рассуждений приходим к определению и уравнению касательной.

Определение. Касательной к графику функция в точке называется предельное положение секущей при .

Уравнение касательной в точке имеет вид

, ,

Его часто записывают иначе

Используя условие ортогональности прямых с угловыми коэффициентами : , получим уравнение Нор-Мали в точке :

Пример. Найти уравнения касательной и нормали к параболе в точке .

- уравнение касательной,

- уравнение нормали.

< Предыдущая		Следующая >